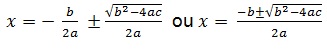A aplicação metodológica da fórmula de Bháskara - parte 2

1.2 Principal contribuição de Bháskara Akaria na construção e desenvolvimento do pensamento matemático: A Fórmula de Bháskara

O que hoje conhecemos no Brasil por fórmula de Bháskara não é comprovado pelos escritos e estudos descobertos por pesquisadores. As seguintes equações referentes ao estudo do seno e cosseno foram concebidas por ele:
sen(a+b)= sen a .cos b + sen b .cos a
sen(a-b) = sen a .cos b - sen b .cos a

O nome Fórmula de Bháskara foi criado para homenagear o matemático que até hoje é considerado o mais importante matemático do século XVI e o último matemático medieval da índia. Essa fórmula é muito significativa e sua importância é notória, pois nos permite resolver qualquer problema que envolva equações quadráticas, as quais aparecem em várias situações, como por exemplo, na Física.

A fórmula de Bhaskara é usada, principalmente, para resolver equações quadráticas de fórmula geral ax² + bx + c = 0, com coeficientes reais, com a ≠ 0. É através desta fórmula que podemos deduzir uma expressão para a soma (S) e o produto (P) das raízes da equação do 2º grau. A fórmula de Bhaskara é a seguinte:

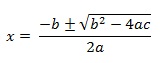
Veja agora como essa fórmula se originou, partindo da fórmula geral das equações de 2º grau:
ax² + bx + c = 0
com a diferente de zero;

Primeiro, multiplicamos todos os membros por 4a:
4a²x² + 4abx + 4ac = 0;

Em seguida, somamos b² em ambos os membros:
4a²x² + 4abx + 4ac + b² = b²;

Após isso, reagrupamos:
4a²x² + 4abx + b² = b² – 4ac

Se observar, o primeiro membro é um trinômio quadrado perfeito:
(2ax + b)² = b² – 4ac

Tiramos a raiz quadrada dos dois membros e colocando a possibilidade de uma raiz negativa e uma positiva:

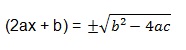
Em seguida, isolamos a incógnita x:

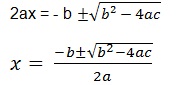
É possível ainda fazer essa fórmula de outra maneira, veja:

Ainda tendo como início a fórmula geral das equações de 2º grau, temos:
ax² + bx + c = 0

Onde a, b e c, são números reais, com a ≠0. Podemos dizer então que:
ax² + bx = 0 – c
ax² + bx = – c

Dividindo os dois lados da igualdade por a, temos:

O objetivo agora é completar os quadrados do lado esquerdo da igualdade. Desta forma será necessário somar  dos dois lados da igualdade:

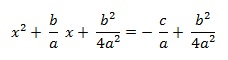
Desta forma, podemos reescrever o lado esquerdo da igualdade da seguinte forma:

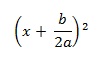
Podemos reescrever também o lado direito da igualdade efetuando a adição das duas frações:

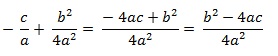
Com isso, ficamos com a seguinte igualdade:

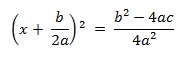
Extraindo a raiz quadrada dos dois lados, temos:

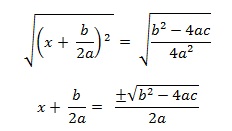
Se isolarmos x, teremos:

<< Página anterior     Próxima página >>