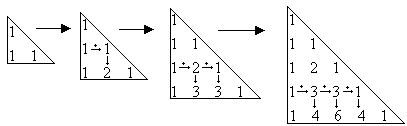Triângulo de Pascal

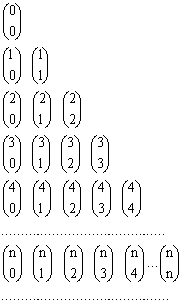
Nesta tabela triangular, os números binomiais com o mesmo numerador são escritos na mesma linha e os de mesmo denominador, na mesma coluna.

Por exemplo, os números binomiais , , e estão na linha 3 e os números binomiais , , , , ..., , ... estão na coluna 1.

Substituindo cada número binomial pelo seu respectivo valor, temos:

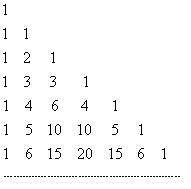
Construção do triângulo de Pascal

Para construir o triângulo do Pascal, basta lembrar as seguintes propriedades dos números binomiais, não sendo necessário calculá-los:

1ª) Como = 1, todos os elementos da coluna 0 são iguais a 1.

2ª) Como = 1, o último elemento de cada linha é igual a 1.

3ª) Cada elemento do triângulo que não seja da coluna 0 nem o último de cada linha é igual à soma daquele que está na mesma coluna e linha anterior com o elemento que se situa à esquerda deste último (relação de Stifel).

Observe os passos e aplicação da relação de Stifel para a construção do triângulo: