Você está em Ensino fundamental > Equações do 2º grau ▼
📄 O que é uma equação do 2º grau?
📄 Raízes de uma equação do 2º grau
📄 Resolução de equações incompletas
📄 Resolução de equações completas
📄 Discriminante
📄 Equações literais
📄 Relações entre os coeficientes e as raízes
📄 Composição de uma equação de 2º grau
📄 Forma fatorada
📄 Equações biquadradas
📄 Resolução de uma equação biquadrada
📄 Composição da equação biquadrada
📄 Equações irracionais
📄 Sistemas de equações do 2º grau
📄 Problemas do 2º grau
📄 Outros exemplos
📄 Raízes de uma equação do 2º grau
📄 Resolução de equações incompletas
📄 Resolução de equações completas
📄 Discriminante
📄 Equações literais
📄 Relações entre os coeficientes e as raízes
📄 Composição de uma equação de 2º grau
📄 Forma fatorada
📄 Equações biquadradas
📄 Resolução de uma equação biquadrada
📄 Composição da equação biquadrada
📄 Equações irracionais
📄 Sistemas de equações do 2º grau
📄 Problemas do 2º grau
📄 Outros exemplos
Raízes de uma equação do 2º grau
Resolver uma equação do 2º grau significa determinar suas raízes.
Raiz é o número real
que, ao substituir a incógnita de uma equação, transforma-a numa
sentença verdadeira. |
O conjunto formado pelas raízes de uma equação denomina-se conjunto verdade ou conjunto solução. Exemplos:
- Dentre os elementos do conjuntos A= {-1, 0, 1,
2}, quais são raízes da equação
x² - x - 2 = 0?
Solução:
Substituímos a incógnita x da equação por cada um dos elementos do conjunto e verificamos quais as sentenças verdadeiras.Para x = -1 (-1)² - (-1) - 2 = 0
1 + 1 - 2 = 0
0 = 0(V) Para x = 0 0² - 0 - 2 = 0
0 - 0 -2 = 0
-2 = 0(F) Para x = 1 1² - 1 - 2 = 0
1 - 1 - 2 = 0
-2 = 0(F) Para x = 2 2² - 2 - 2 = 0
4 - 2 - 2 = 0
0 = 0(V) Logo, -1 e 2 são raízes da equação.
- Determine p sabendo que 2 é raiz da equação (2p
- 1) x²
- 2px
- 2 = 0.
Solução:
Substituindo a incógnita x por 2, determinamos o valor de p.
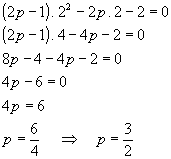
Logo, o valor de p é
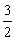 .
.
Próximo: Resolução de equações incompletas
Como referenciar: "Equações do 2º grau" em Só Matemática. Virtuous Tecnologia da Informação, 1998-2024. Consultado em 21/11/2024 às 04:49. Disponível na Internet em https://www.somatematica.com.br/fundam/equacoes2/equacoes2_2.php





























