📄 Domínio e imagem das funções inversas
📄 Gráficos das funções inversas
📄 Funções logarítmica e exponencial
📄 Logaritmos
📄 Funções logarítmicas
📄 Funções definidas explicitamente e implicitamente
📄 Diferenciação implícita
📄 Derivadas de potências racionais de x
📄 Derivadas de funções logarítmicas
📄 Diferenciação logarítmica
📄 Derivadas de funções exponenciais
📄 Derivadas das funções trigonométricas inversas
Funções Logarítmica e Exponencial
Antes de estudarmos estes dois tipos de funções, vamos entender o que são funções inversas.
Funções inversas
Em linguagem comum, o termo "inversão" transmite a ideia de uma reversão. Por exemplo, em meteorologia, a inversão da temperatura é uma reversão nas propriedades usuais da temperatura de camadas de ar; em música, uma inversão é um tema recorrente que usa as mesmas notas na ordem reversa. Em matemática, o termo inversa é usado para descrever funções que são reversas uma da outra, no sentido que cada uma desfaz o efeito da outra.
A ideia de resolver uma equação y = f (x) para x com uma função de y, digamos x = g(y), é uma das ideias mais importantes da matemática. Às vezes, resolver esta equação é um processo simples; por exemplo usando álgebra básica, a equação
y = f (x)
pode ser resolvida para x como uma função de y:
x = g (y)
A primeira equação é melhor para calcular y se x for conhecido, e a segunda é melhor para calcular x se y for conhecido
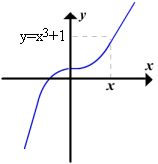
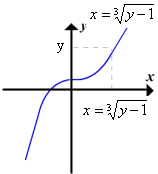
O interesse fundamental é identificar relações que possam existir entre as
funções f e g, quando uma função y=f(x)
for expressa como x = g(y), ou ao contrário. Por exemplo,
consideremos as funções 
e 
discutidas
acima. Quando funções forem compostas em qualquer ordem, uma cancela o efeito
da outra significando que
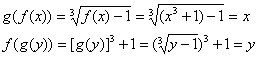
A primeira dessas equações estabelece que cada saída de uma composição g(f(x)) é igual à entrada, e a segunda estabelece que cada saída da composição f(g(y)) é igual à entrada. Os pares de funções com essas duas propriedades são tão importantes que há uma terminologia específica para elas.
| Se as funções f e g satisfazem as duas
condições
g(f(x)) = x para todo x no domínio de f f(g(y)) = y para todo y no domínio de g então, dizemos que f e g são funções inversas. Além disso, chamamos f uma inversa de g e g uma inversa de f. |
Exemplo
Confirme cada um dos seguintes itens.
(a) A inversa de 
(b) A inversa de 
Solução (a).
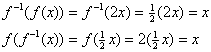
Solução (b).
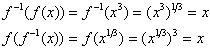
OBSERVAÇÃO.
O resultado no exemplo deve fazer sentido
intuitivamente para você, uma vez que as operações de multiplicar por 2 e
multiplicar por 
em qualquer ordem cancelam uma o efeito da outra, da mesma que as operações de
elevar ao cubo e extrair a raiz cúbica.
