|
Funções
Logarítmica e Exponencial
- DERIVADAS DE POTÊNCIAS RACIONAIS DE X
A partir da equação que segue, mostramos que a
fórmula
é válida para todos os valores inteiros de n e
para n =  . Usaremos agora a diferenciação implícita para mostrar
que esta fórmula é válida para qualquer expoente racional. Mais precisamente,
mostraremos que se r for um número racional, então
sempre que 
e 
estiverem definidas. Por ora, admitiremos, sem prova que
é
diferenciável.
Seja y =
. Uma vez que r é um
número racional, pode ser expresso como uma razão de inteiros r = m/n.
Assim, y = =
pode
ser escrito como
Diferenciando implicitamente em relação a x e
usando , obtemos
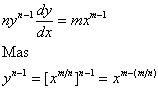
Desta forma, pode ser escrito como
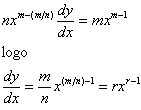
Exemplo
A partir de
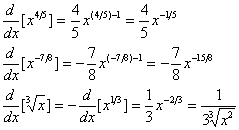
Se u for uma função diferenciável de x
e r for um número racional, então a regra da cadeia dá lugar à
seguinte generalização de
<<
Voltar para Ensino Superior
|
