A irrazoável efetividade da matemática (IV)
Português e matemática compartilham características comuns enquanto linguagens, como a capacidade de serem usadas para fazer diferentes tipos de previsões. A descrição matemática parece mais adequada a informações quantitativas, enquanto que o português pode ter expressões qualitativas superiores.
Entretanto, a matemática é uma linguagem que contém muitas sublinguagens que possuem conexões entre si: geometria, álgebra, topologia, etc. Portanto, a matemática oferece uma descrição muito mais ampla e não homogênea como coleção de sublinguagens.
Assim, a descrição matemática consiste de narrativas complexas muito mais amplas do que as descrições restritas à linguagem do português.
Quando usamos matemática como linguagem para descrever um processo, nós, antes de tudo, criamos um estoque rico de narrativas possíveis da matemática, sem nos preocupar com quais delas se ajustarão bem aos objetos do mundo natural.
Entretanto, o papel da forma na matemática é extremamente sugestivo.
A estratégia básica é que, olhando o modo pelo qual as expressões, as equações e diagramas são escritos e representados, e aparecem no curso da imaginação matemática, estamos aptos a identificar novas imaginações.
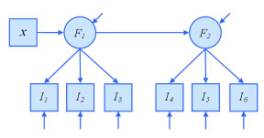
Uma representação como esta figura pode descrever relações, causais ou não, entre variáveis não observáveis (latentes) F1 e F2, medidas por meio de indicadores observáveis Ij. Structural Equation Models (SEM´s) são modelos matemático-estatísticos usados para avaliar se modelos teóricos são plausíveis quando comparados com dados “observados”. SEM´s são muito gerais de modo que, por exemplo, análise de regressão e análise fatorial são ambas justamente casos particulares seus.
Uma teoria nas ciências sociais tende a ser muito rica e complexa, onde múltiplos resultados são vistos como conseqüências de múltiplos fatores interagindo em cadeias de mediação. A análise de regressão padrão não pode representar tais teorias em um modelo único, forçando o pesquisador a avaliar apenas modelos parciais ou muito restritos. Os SEM´s, por sua vez, permitem representar uma teoria complexa em um modelo único e integrado.
SEM´s permitem que os pesquisadores considerem seriamente os problemas de modelagem de construtos hipotéticos. Embora às vezes não reconhecidos enquanto tais, muitos dos fenômenos de interesse nas ciências sociais não são diretamente observáveis, mesmo em princípio, mas são, ao invés disso, construtos hipotéticos, artifícios intelectuais que são usados para categorizar e dar significado a fenômenos observados. Exemplos incluem o capital social, o autoritarismo, os cartéis e as classes sociais. SEM´s permitem aos pesquisadores representar esses construtos hipotéticos explicitamente e distinguir a mensuração de um construto das relações entre os construtos.
Portanto, o papel da matemática nas ciências sociais parece ser essencialmente dependente da possibilidade de se usar os símbolos matemáticos como figuras.
Analogamente, a geração de “alfabetos” em matemática é em si mesmo um processo muito criativo, e muitas vezes sugerem os tipos de imaginações que podemos produzir com eles.
Por exemplo, o alfabeto dos SEM´s com suas variáveis latentes, manifestas, de perturbação, e suas flechas de relações, sugerem certos tipos de causalidade em ciências sociais.
O MJVI, como estratégia no jogo do Ser, imagina que a matéria viva não possa interromper o impulso de vida que teria se seguido, provavelmente, de um impulso gerado em uma instabilidade do “NADA”.
Mesmo porque, inspirado em Sigmund Freud, imagina um incentivo irresistível para o Ser da vida que é nada mais do que um Princípio de Prazer pressionando avassaladoramente a matéria para que se transforme em informação, ou mais precisamente, em imaginações. A pressão resulta no mistério de imaginações que imaginam e que se imaginam, abrindo, assim, caminho para a imaginação crucial, o desejo, maior de todos, de existir da autoconsciência.
Prazeres e desprazeres “corpóreos” não são suficientemente convincentes para que o MJVI inclua, em suas estratégias no jogo do Ser, a imaginação de que o objetivo desse jogo pudesse ser a existência eterna.
Não esquece, sobretudo, a sutil imaginação da dúvida hiperbólica de Descartes para descobrir, enfim, magistralmente diga-se, que “penso”.
O MJVI põe-se, entretanto, modestamente na posição mais prudente “imagino, apenas”!





























