Leonhard Euler

No período de aproximadamente 100 anos, que sucedeu o ano de 1650, a Teoria dos Números ficou adormecida. Esse período foi marcado por um desenvolvimento indescritível na ciência devido ao surgimento do Cálculo e o seu conseqüente desenvolvimento denominado de Análise Matemática por Issac Newton (1646–1716), Gottfried Wilhelm Leibniz (1646-1716), a família  Bernoulli (Jacob, 1655-1705; Johann I, 1667-1748; Nicholas II, 1687-1759; Daniel 1700-1792), e Leonhard Euler (1707-1783).

No final do Século XVI o cientista italiano Galileu Galilei inaugurou a Ciência, no sentido moderno do termo, pois foi o primeiro a realizar experimentos de forma ordenada e sistemática, supondo que a Natureza obedece a leis matemáticas, descobrindo dessa forma algumas leis da natureza formuladas matematicamente.

Galileu seguia a concepção dos filósofos da Grécia Antiga e, portanto, para ele, Matemática significava Geometria Euclidiana, enquanto que Ciência significava “Filosofia Natural”. Sob essa visão problemas matemáticos eram geometrizados, ou seja, procuravam-se soluções em termos de construções geométricas.

Contudo na época de Galileu a Álgebra já havia sido introduzida na Europa. Desenvolvida por filósofos islâmicos da Pérsia, que por sua vez haviam aprendido com os matemáticos indianos, a palavra Álgebra foi derivada do árabe al-gabr (“ligar conjuntamente”) e essa concepção se resumia no seguinte processo:

“redução do número de quantidades desconhecidas ligadas ao problema que se deseja resolver e, a seguir, ligá-las conjuntamente em um sistema denominado de equação,     sendo o passo seguinte o de se encontrar a solução da equação”.

Coube ao brilhante filósofo e matemático René Descartes a unificação da Geometria e da Álgebra. Assim, concepções distintas criadas para resolver problemas matemáticos que provinham de culturas distintas deram origem a uma das maiores invenções da Matemática:

“A Geometria Analítica”.

A Geometria Analítica consistia de um método que tornava as equações algébricas “visíveis” como formas geométricas. Por exemplo, a equação x + y = 1, passava a ter uma representação geométrica, ou seja, a equação era representada graficamente por uma reta.                

A representação gráfica de uma equação algébrica correspondia a um ente da geometria. Uma reta não estava mais localizada no plano de Euclides, mas sim no plano cartesiano formulado por Descartes. Analogamente, equações envolvendo x e y correspondiam às curvas no plano cartesiano. Por exemplo, à equação x² + y²  = 1 correspondia no plano cartesiano uma circunferência de centro na origem (0,0) e raio unitário.

Essa invenção de Descartes permitiu que Galileu formulasse as leis da mecânica que descobriu, tanto algebricamente como geometricamente. Contudo um problema permanecia: como encontrar uma equação que descrevesse o movimento de um corpo animado de velocidade variável, acelerado ou desacelerado? Ou seja, Galileu e seus contemporâneos não eram capazes de expressar, matematicamente, a velocidade exata de um corpo com aceleração num dado instante, pois a velocidade mudava a cada instante.

Coube ao gênio da ciência clássica Isaac Newton, e ao matemático e filósofo alemão Gottfried Wilhelm Leibniz, resolver essa questão que atormentava matemáticos e filósofos por vinte séculos, desde os sofistas gregos.

De modo independentemente, Newton e Leibniz, um século após Galileu, inventaram um método genial que daria fim a essa questão. Nascia o Cálculo Diferencial e Integral que se mostraria uma das maiores aquisições intelectuais do mundo ocidental.

Os métodos da Análise Matemática sempre desempenharam um papel fundamental na pesquisa em Teoria dos Números. Essa parceria entre Análise e Teoria dos Números tem suas origens no trabalho de Euler e foi amplamente desenvolvimento pelo matemático L. P. G. Dirichlet.(1805-1859).

Leonhard Euler foi um dos maiores matemáticos de todos os tempos. Ele publicou aproximadamente 500 artigos em vida e, aproximadamente, 350 artigos póstumos apareceram. Apesar de ter ficado cego de um olho quando jovem, e ter ficado completamente cego aos sessenta anos, ele trabalhou em praticamente todas as áreas da Matemática e da Física. Além disso, escreveu livros notáveis sobre Álgebra, Trigonometria, Cálculo, Mecânica, Dinâmica, Cálculo de Variações, Astronomia, Artilharia, Ótica e muito mais.

Sua investigação original foi fundamental para a Matemática dos Séculos XVIII e XIX devido à sua criatividade, inspiração e genial capacidade de unificar e sistematizar todo o conhecimento produzido até então.

Euler foi o primeiro matemático a aplicar as idéias da Análise a problemas de Teoria dos Números. Na verdade, como se observou posteriormente, ele estava utilizando técnicas da Teoria das Funções Complexas. Dessa forma, atacou dois problemas fundamentais da Teoria dos Números.

O primeiro problema da Teoria dos Números em que Euler aplicou os métodos analíticos diz respeito a soluções inteiras de equações. Para determinar as soluções inteiras de uma equação linear, Euler criou um método que se tornou conhecido como Método das Funções Geradoras (Generating Functions).

O método das funções geradoras se mostrou tão genial que levou à criação do Método do Círculo de Hardy-Littlewood-Ramanujan (Circle Method) cujo desenvolvimento, por sua vez, levou a um dos métodos básicos da Teoria Analítica dos Números Contemporânea: o método das somas trigonométricas de Vinogradov (Method of Trigonometric Sums).  Essa idéia levou à criação do ramo da Teoria Analítica dos Números conhecida como “Teoria Aditiva dos Números”.

O outro problema se relacionava com o comportamento da seqüência de números primos no conjunto dos números inteiros positivos. Euler deu uma nova demonstração do Teorema de Euclides sobre a existência de infinitos números primos baseando-se em argumentos analíticos. A idéia de Euler mostrou-se bastante frutífera e deu ímpeto ao desenvolvimento de uma linha importante de pesquisa em Teoria Analítica dos Números: a “Teoria Multiplicativa dos Números”.

A fórmula

foi descoberta por Euler aproximadamente em 1735.

Euler ficou bastante satisfeito em demonstrar o fato misterioso de que essa soma relaciona-se ao número . Na verdade, a identidade acima representa um valor especial calculado em uma classe de funções chamada de Funções Zeta (“zeta functions”).

Observe que, se demonstrarmos que z define uma função, então

.

Euler demonstrou que para todo número real s > 1, a série

define a função

denominada função zeta.

Euler demonstrou a existência de um número infinito de números primos utilizando-se das propriedades analíticas dessa função. Existe uma relação entre a Função Zeta e o conjunto dos números primos denominada de Produto de Euler. O produto de Euler é uma expressão analítica da fatoração única de inteiros como produto de números primos: 

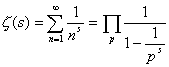
para s > 1, onde o produto à direita é tomado para todos os números primos.

È interessante observar que o Produto de Euler implica, em particular, que

para s > 1.

A Função Zeta introduzida por Euler se revelou um dos personagens mais importantes da Teoria dos Números, pois apresenta propriedades aritméticas preciosas. Alguns matemáticos costumam dizer que Teoria dos Números é o estudo de Funções Zeta.

No Século XIX o matemático Bernard Riemann definiu a Função Zeta no conjunto dos números complexos e, devido às suas inúmeras e fundamentais contribuições ao estudo dessa função, hoje ela é conhecida como “Função Zeta de Riemann”.

Uma nova jornada se iniciava com Riemann. Ele fez uma conjectura denominada  Hipótese de Riemann que até hoje é um dos maiores desafios para os matemáticos mais brilhantes. A Hipótese de Riemann será o tema de nossas próximas colunas.