Conjectura de Poincaré

Formulada no início do século XX pelo matemático francês Henri Poincaré, a conjectura de Poincaré é um dos mais famosos problemas da Matemática.

Ela afirma que a superfície tridimensional de uma esfera é o único espaço fechado de dimensão 3 onde todos os contornos ou caminhos podem ser encolhidos até chegarem a um simples ponto. Durante o século XX, a conjectura de Poincaré motivou avanços notáveis na Geometria e na Topologia.

Este problema permaneceu em aberto durante cerca de cem anos. Enfim, no final de 2003, o matemático russo Grigori Perelman começou a publicar na internet uma série de artigos científicos que continham a solução do problema. O matemático recusou-se a receber a Medalha Fields, assim como o prêmio Clay no valor de um milhão de dólares.

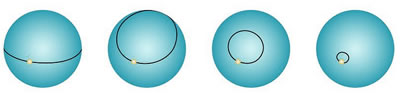
O círculo de dimensão 2 (em preto na figura) pode ser compactado até se tornar um ponto. A conjectura de Poincaré afirma que isso também vale para uma esfera de dimensão 3.

O Clay Mathematics Institute anunciou em 18 de março de 2010 que o Dr. Grigori Perelman era o vencedor de um dos sete Problemas do Prémio Millenium.

Perelman, que reside em São Petersburgo, se nega a falar com a imprensa e evita aparecer em público. Na única oportunidade em que se pronunciou, ele disse porque não aceitou o prêmio ou qualquer condecoração: "Eu não sou um herói da matemática. Eu não fiz nada de excepcional, e eu não quero ser observado por todo o mundo. Eu tenho tudo o que eu quero e parem de me perseguir, VTC...!". Logicamente, "VTC" é um palavrão, o que demonstra sua irritação por se considerar tão perseguido pelo seu feito.