Solução de uma equação do 1º grau com duas variáveis

Quais o valores de x e y que tornam a sentença x - 2y = 4 verdadeira?

Observe os pares abaixo:

x = 6,  y = 1

x - 2y = 4

6 - 2 . 1 = 4

6 - 2 = 4

4 = 4  (V)

x = 8,  y = 2

x - 2y = 4

8 - 2 . 2 = 4

8 - 4 = 4

4 = 4  (V)

x = -2,  y = -3

x - 2y = 4

-2 - 2 . (-3) = 4

-2 + 6 = 4

4 = 4  (V)

Verificamos que todos esses pares são soluções da equação x - 2y = 4. Assim, os pares (6, 1); (8, 2); (-2, -3) são algumas das soluções dessa equação.

Uma equações do 1º grau com duas variáveis tem infinitas soluções - infinitos (x, y) -, sendo portanto seu conjunto universo .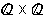

Podemos determinar essas soluções atribuindo-se valores quaisquer para uma das variáveis, calculando a seguir o valor da outra. Exemplo:

• Determine uma solução para a equação 3x - y = 8.

Atribuímos para x o valor 1, e calculamos o valor de y. Assim:

3x - y = 8

3 . (1) - y = 8

3 - y = 8

-y = 5  ==> Multiplicamos por -1

y = -5

O par (1, -5) é uma das soluções dessa equação.

V = {(1, -5)}

Resumindo: