Mínimo múltiplo comum (M.M.C.)

Múltiplo de um número natural

Como 24 é divisível por 3, dizemos que 24 é múltiplo de 3.

24 também é múltiplo de 1, 2, 3, 4, 6, 8, 12 e 24.

Se um número é divisível por outro, diferente de zero, então
dizemos que ele é múltiplo desse outro.

Os múltiplos de um número são calculados multiplicando-se esse número pelos números naturais.

Exemplo: os múltiplos de 7 são:
7x0 , 7x1, 7x2 , 7x3 , 7x4 , ... = 0 , 7 , 14 , 21 , 28 , ...

Observações importantes:
1) Um número tem infinitos múltiplos
2) Zero é múltiplo de qualquer número natural

O que é M.M.C.?

Dois ou mais números sempre têm múltiplos comuns a eles. Vamos achar os múltiplos comuns de 4 e 6:
Múltiplos de 6: 0, 6, 12, 18, 24, 30,...
Múltiplos de 4: 0, 4, 8, 12, 16, 20, 24,...
Múltiplos comuns de 4 e 6: 0, 12, 24,...

Dentre estes múltiplos, diferentes de zero, 12 é o menor deles. Chamamos o 12 de mínimo múltiplo comum de 4 e 6.

O menor múltiplo comum de dois ou mais números, diferente de zero, é chamado de mínimo múltiplo comum desses números. Usamos a abreviação m.m.c.

Cálculo do M.M.C.

Podemos calcular o m.m.c. de dois ou mais números utilizando a fatoração. Acompanhe o cálculo do m.m.c. de 12 e 30:

1º) decompomos os números em fatores primos
2º) o m.m.c. é o produto dos fatores primos comuns e não-comuns:

12 = 2 x 2 x 3
30 = 2 x 3 x 5
m.m.c (12,30) = 2 x 2 x 3 x 5

Escrevendo a fatoração dos números na forma de potência, temos:
12 = 2² x 3
30 = 2 x 3 x 5
m.m.c (12,30) = 2² x 3 x 5

O m.m.c. de dois ou mais números, quando fatorados, é o produto dos fatores comuns e não-comuns a eles, cada um elevado ao maior expoente.

Processo da decomposição simultânea

Neste processo, decompomos todos os números ao mesmo tempo, em um dispositivo como mostra a figura ao lado. O produto dos fatores primos que obtemos nessa decomposição é o m.m.c. desses números. A seguir vemos o cálculo do m.m.c.(15,24,60).

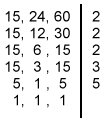
Portanto, m.m.c.(15,24,60) = 2 x 2 x 2 x 3 x 5 = 120

Propriedade do M.M.C.

Entre os números 3, 6 e 30, o número 30 é múltiplo dos outros dois. Neste caso, 30 é o m.m.c.(3,6,30). Observe:

m.m.c.(3,6,30) = 2 x 3 x 5 = 30

Dados dois ou mais números, se um deles é múltiplo de todos os outros, então ele é o m.m.c. dos números dados.

Considere os números 4 e 15, que são primos entre si. O m.m.c.(4,15) é igual a 60, que é o produto de 4 por 15. Observe:

m.m.c.(4,15) = 2 x 2 x 3 x 5 = 60

Dados dois números primos entre si, o m.m.c. deles é o produto desses números.

Próximo conteúdo: Equações do 1º grau com uma variável