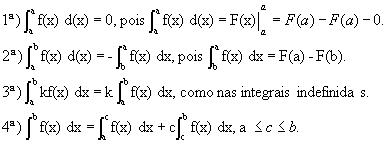Cálculo da integral definida

O método que temos para o cálculo da área ou da integral definida, no caso, é ainda muito complicado, conforme vimos no exemplo anterior, pois encontraremos somas bem piores.

Para tal, consideremos a área das figuras quando movemos a extremidade direita:

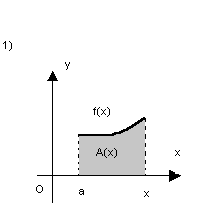
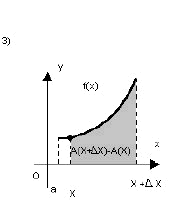
Se a área é dada por A(x), então A(a) = 0, pois não há área alguma. Já A(x) dá a área da figura 1, A(b), a área entre ou seja:

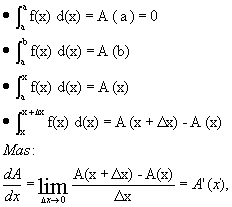
ou seja, A(x) é uma das antiderivadas de f(x). Mas sabemos que se F(x) é antiderivada qualquer de f(x), então A(x) = F(x) + C. Fazendo x = a, temos: A(a) = F(a) + C = 0 (A(a) = 0)

Logo, C = - F(a) e A(x) = F(x) - F(a).

Portanto:                                                  

ou ainda,  

Exemplos:

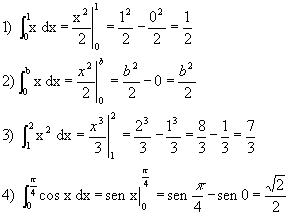
Note que conseguimos uma forma de calcular integrais definidas e áreas sem calcular somas complicadas e usando apenas as antiderivadas.

Propriedades da integral definida