📄 Propriedades dos Limites
📄 Limites Laterais, Continuidade
📄 Limites envolvendo infinito
📄 Limites trigonométricos
📄 Limites exponenciais
Limites
Noção intuitiva de limite
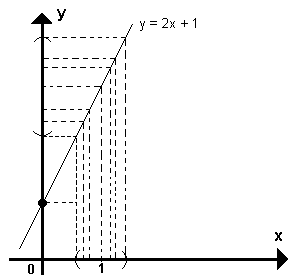
Seja a função f(x)=2x+1. Vamos dar valores a x que se aproximem de 1, pela sua direita (valores maiores que 1) e pela esquerda (valores menores que 1) e calcular o valor correspondente de y:
| x | y = 2x + 1 |
| 1,5 | 4 |
| 1,3 | 3,6 |
| 1,1 | 3,2 |
| 1,05 | 3,1 |
| 1,02 | 3,04 |
| 1,01 | 3,02 |
x |
y = 2x + 1 |
| 0,5 | 2 |
| 0,7 | 2,4 |
| 0,9 | 2,8 |
| 0,95 | 2,9 |
| 0,98 | 2,96 |
| 0,99 | 2,98 |
Notamos que à medida
que x se
aproxima de 1, y
se aproxima de 3, ou seja, quando x
tende para 1 (x![]() 1), y tende para
3 (y
1), y tende para
3 (y ![]() 3), ou seja:
3), ou seja:
Observamos que quando x tende para 1, y tende para 3 e o limite da função é 3.
Esse é o estudo do comportamento de f(x)
quando x tende
para 1 (x ![]() 1). Nem é
preciso que x assuma
o valor 1. Se f(x)
tende para 3 (f(x)
1). Nem é
preciso que x assuma
o valor 1. Se f(x)
tende para 3 (f(x)
![]() 3),
dizemos que o limite de f(x)
quando x
3),
dizemos que o limite de f(x)
quando x ![]() 1 é 3, embora possam ocorrer casos em que para x =
1 o valor de f(x)
não seja 3.
De forma geral, escrevemos:
1 é 3, embora possam ocorrer casos em que para x =
1 o valor de f(x)
não seja 3.
De forma geral, escrevemos:
se, quando x se
aproxima de a (x
![]() a), f(x)
se aproxima de b
(f(x)
a), f(x)
se aproxima de b
(f(x)![]() b).
b).
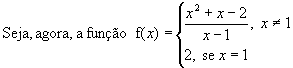
Como x² + x - 2 = (x - 1)(x + 2), temos:
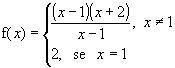
Podemos notar que quando x
se aproxima de 1 (x![]() 1),
f(x) se aproxima
de 3, embora para x=1
tenhamos f(x) =
2. o que ocorre é que procuramos o comportamento de y
quando x
1),
f(x) se aproxima
de 3, embora para x=1
tenhamos f(x) =
2. o que ocorre é que procuramos o comportamento de y
quando x![]() 1.
E, no caso, y
1.
E, no caso, y ![]() 3. Logo, o limite de f(x)
é 3.
3. Logo, o limite de f(x)
é 3.
Escrevemos:
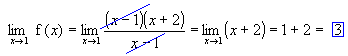
Se g: IR ![]() IR e g(x) = x
+ 2,
IR e g(x) = x
+ 2, ![]() g(x)
=
g(x)
= ![]() (x
+ 2) = 1 + 2 = 3, embora g(x)
(x
+ 2) = 1 + 2 = 3, embora g(x)![]() f(x)
em x = 1. No
entanto, ambas têm o mesmo limite.
f(x)
em x = 1. No
entanto, ambas têm o mesmo limite.