Uso de Jogos e Materiais Manipuláveis no Ensino de Matemática nos Anos Finais do Ensino Fundamental (página 5)

5. TIPOS DE JOGOS E ATIVIDADES QUE PODEM SER UTILIZADAS NAS SÉRIES FINAIS DO ENSINO FUNDAMENTAL (6º AO 9º ANO).

Neste tópico serão apresentados alguns jogos que podem ser utilizados nos anos finais do ensino fundamental seguindo três eixos temáticos da nova base nacional comum curricular. Os jogos serão separados por série, e em cada jogo será especificado o eixo temático, ou seja, se o jogo é sobre números, geometria ou álgebra.

Jogos para o sexto ano:

1. Com o objetivo de contribuir com o eixo temático associado aos números no sexto ano, podemos utilizar o bingo dos múltiplos e divisores. O jogo é composto por um quadro numerado como a que segue abaixo de 2 a 50 e de dois marcadores de conjunto de cores diversas que podem ser constituídos de tampinhas de frasco plástico de refresco.

Quadro 1: Quadro numerado de 2 a 50

A finalidade deste material é utilizar os ideias de múltiplos e divisores na resolução de questões. Para que o jogo seja realizado serão formados dois grupos, e suas regras são:
1 – Seleciona-se a primeira equipe para jogar;
2 – O primeiro grupo aponta um número mostrando com o seu marcador;
3 – Já o segundo grupo marcará com seu registro os divisores e múltiplos do número marcado pelo opositor e mais um novo número;
4 – Se um participante do jogo retirar um número que jamais é divisor do último número indicado pelo oponente, então, este número será conhecido como o último número;
5 – Todo número só poderá ser marcado uma única vez;
6 – Um participante não poderá estabelecer números após ter passado a sua vez;
7 – A rodada acaba à medida que todos os números são marcados;
8 – Os pontos de cada participante serão obtidos pela reunião de todos os resultados que ele estabeleceu.

b) A fim de praticarmos a geometria em conformidade com o sexto ano podemos pensar em executar com o batalha da simetria . O objetivo desta batalha é introduzir e entender a conhecimento de simetria. O material necessário é uma folha de papel sulfite e duas canetas. Esta tarefa pode ser efetuada em duplas e apresenta as seguintes regras:

1 – Dobrar a folha de papel sulfite ao meio. Cada  metade corresponderá a um praticante da atividade,
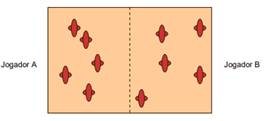
2 – Cada jogador desenhará 5 aviões pequenos em alguma parte da sua metade de papel (figura abaixo).

Figura 1: desenho dos aviões na folha A3.

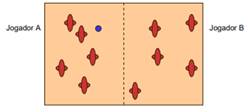
3 – Na primeira jogada, o jogador A fará, em sua metade de papel, um ponto localizado simetricamente a um dos aviões feito pelo jogador B.

Figura 2: Representação do ponto feito pelo jogador A simétricamente a folha do jogador adversário.
 

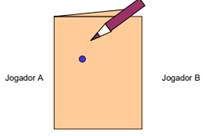
4 – Dobra-se então a folha e rabisca-se atrás do ponto feito pelo jogador A.

 

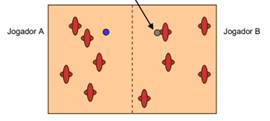
5 – Desdobrar a folha e verificar se o ponto atingiu o avião do adversário.

6 – O mesmo será feito pelo jogador B.
7 – Ganhará o jogo quem atingir primeiro os cinco aviões do adversário.

Jogos para o sétimo ano:

a) Com o objetivo de executar o eixo temático dos números com sétimo ano, podemos apresentar uma tarefa usando um jogo para trabalhar os números positivos e negativos. O jogo que pode ser empregado é o matix.
Para este jogo são importantes os seguintes instrumentos: um tabuleiro (igual ao de damas ou xadrez), de acordo com a figura 5 e 64 fichas com números negativos e positivos (conforme relação abaixo).

Figura 5: Tabuleiro de xadrez
 

Quadro 2: quadro com números positivos e negativos retirada do site da UNESP.

O objetivo do jogo é adquirir o maior número de pontos. Suas regras são:
1 - Distribui-se por acaso em um tabuleiro números positivos e negativos e um coringa. Antes de começar os grupos precisam determinar quem será a linha e qual será a coluna.
2 – Tira-se par ou ímpar para resolver quem iniciará o desafio.
3 - A equipe que começar o desafio, deve tirar o coringa e a partir dele começar o jogo. Se a equipe for coluna, por exemplo, ela deve eliminar um número da coluna que havia o coringa, juntando então seus primeiros pontos.
4 - Em seguida é a vez da outra equipe, ela deve tirar um número da linha onde a outra equipe havia tirado, completando assim seus primeiros pontos. Em continuidade é a vez da equipe coluna tirar um número da coluna onde a outra equipe havia extraído, completando assim seus primeiros pontos. Em seguida é a vez da equipe coluna tirar um número da coluna em que a equipe posterior equipe havia retirado, e do mesmo modo posteriormente.
5 - O jogo termina caso não houver mais números para serem tirados na coluna ou na linha e o ganhador será quem tiver o maior número de cartas.

b) Para manusear a álgebra junto com o sétimo ano julguei importante trazer um jogo com o objetivo de que os estudantes entendam as equações do 1º grau. O jogo que pode ser utilizado para esse conteúdo é o jogo de dama das equações do primeiro grau, cujos objetivos são resolver equações e despertar o pensamento lógico do estudante.
Para a realização da atividade, a classe será dividida em grupos de dois alunos. O material utilizado por cada dupla será um tabuleiro 8 x 8 com 64 casas (figura abaixo).

Figura 6: tabuleiro para jogo de damas de equações do primeiro grau.
 

Esta competição é formada pelas seguintes regras:
1 – O jogador que iniciar a partida escolherá uma peça arbitrariamente e resolverá sua equação e o valor (raiz da equação) da incógnita será o valor de seus pontos, valores os quais se diferenciarão entre negativos, positivos e nulos.
2 – O seguinte participante da atividade só será capaz de retirar peças que existam na mesma coluna e linha da peça já extraída e assim até que as peças do tabuleiro acabem.
3 – Depois do  final do jogo, somam-se os valores das incógnitas das respectivas equações escolhidas e o jogador que atingir a maior pontuação (soma) será o vencedor.

<< Página anterior   Próxima página >>