Uso de Jogos e Materiais Manipuláveis no Ensino de Matemática nos Anos Finais do Ensino Fundamental (página 7)
Jogos para o 9º ano:
a) Para contribuir com o eixo temático números de acordo com o nono ano, podemos usar como atividade lúdica um bingo de potências e raízes. O objetivo deste material é fazer com que por meio desta tarefa, os estudantes desenvolvam seus estudos com relação há potenciação e radiciação. Para que a tarefa aconteça, será fundamental usar os respectivos materiais: Cartelas de cartolina contendo números que sejam resultados das potências/raízes citadas pelo professor. Fazer o número de cartelas conforme o número de alunos da classe. Quadradinhos pequenos de cartolina contendo as potências a serem resolvidas para fazer o sorteio, colocados em um recipiente (sacola plástica ou pote). Grãos para marcar os números sorteados ou lápis para marcar os números.
O bingo das potências e raízes é composto pelas seguintes regras:
1 – Inicialmente cada dupla recebe uma cartela de marcação.
2 – São sorteadas as potencias e as raízes e os alunos devem marcar as respostas referentes às potências ou raízes sorteadas.
- Para trabalhar o eixo temático de álgebra com o nono ano, podemos aplicar uma atividade para que o aluno identifique equações do segundo grau, bem como seus coeficientes e consiga visualizar as equações completas e incompletas. Este jogo é composto de três materiais: um tabuleiro, pinos e cartas de dicas (figuras abaixo). Esta atividade lúdica possui as seguintes regras:

Figura 10: Quadro de dicas.

1 – A turma será dividida em grupos de cinco alunos (um para ler as dicas e os outros para jogar).
2 – Todos os jogadores tem que ter em mãos papel e lápis. O primeiro jogador escolhe um número de 1 a 12 e o aluno que está com a carta de dicas lê a que corresponde ao número escolhido. Os jogadores irão anotar estas dicas para montar a equação escrita na carta.
3 – Em seguida o próximo jogador escolhe outro número de 1 a 12 diferente do escolhido anteriormente. Esse procedimento deverá ser repetido até que um dos jogadores escreva a equação correta.
4 – Vence o jogo aquele aluno que chegar primeiro ao final do caminho.
5 – Esta atividade será avaliada pela participação dos alunos durante as aulas e também por suas anotações feitas durante as jogadas.
6 – Em seguida será feita uma discussão com os alunos sobre o conteúdo trabalhado com o jogo: a definição de equação do 2º grau, seus coeficientes e a classificação em completa ou incompleta.
c) Para trabalhar a geometria como o nono ano podemos utilizar o quebra cabeça pitagórico, cujo objetivo é introduzir o trabalho com o Teorema de Pitágoras. O material necessário para se jogar este jogo é o quebra cabeça de acordo com o modelo abaixo:
Figura 11: modelo de quebra cabeça pitagórico extraído do Programa de cursos 2011
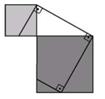
Cada aluno deve receber dez peças, sendo:
Figura 12: Peças do quebra cabeça pitagórico.
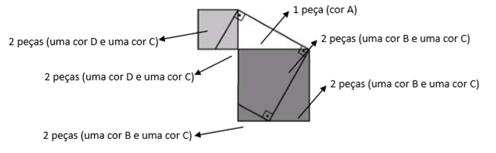
O jogo é formado de um ou dois elementos e possui as seguintes regras:
1 – Solicitar aos alunos que façam as seguintes atividades, utilizando as peças do quebra-cabeça pitagórico.
Atividade 1: Com duas peças da mesma cor e de diferentes formatos, monte uma figura que tenha a forma de um quadrado.
Atividade 2: Com três peças de uma mesma cor, monte uma figura que tenha a forma de um quadrado.
Atividade 3: Com as peças restantes, monte uma figura que tenha a forma de um quadrado.
Atividade 4: Justaponha as três figuras quadradas construídas com as peças aos três lados da figura triangular branca.
Atividade 5: Que relação é possível formar, levando em conta o comprimento dos lados do triângulo retângulo e os lados das figuras justapostas?
Atividade 6: Chamando de “a” a medida da hipotenusa, de “b” a medida do cateto menor e de “c” a medida do outro cateto do triângulo retângulo, o que é possível afirmar, em relação às áreas dos quadrados construídos?
2 – Realizadas as atividades anteriores, encerra-se a atividade.
6. METODOLOGIA
Este estudo tem como base uma pesquisa qualitativa que tem como foco alcançar os objetivos que foram propostos, os quais foram analisar como os materiais manipuláveis podem contribuir no ensino de matemática nos anos finais do ensino fundamental, relatar o que são jogos matemáticos e quais benefícios estes trazem e descrever alguns materiais manipuláveis que sejam de acordo com as áreas dispostas na base nacional comum curricular que podem ser utilizados no ensino de matemática nos anos finais do ensino fundamental.
Casarin (2012, p. 32) afirma que “a pesquisa qualitativa explora uma metodologia predominantemente descritiva, deixando em segundo plano modelos matemáticos e estatísticos. Neste tipo de pesquisa, a quantificação do o objeto estudado não é priorizado”
Primeiramente, foi feita uma revisão bibliográfica em livros, artigos científicos e alguns sites da internet para descrever o uso de Jogos e materiais manipuláveis para o ensino de matemática no ensino fundamental. Por meio destes sites também serão executadas pesquisas de materiais que podem ser utilizados nas aulas de matemática nos anos finais do ensino fundamental seguindo os eixos temáticos números, álgebra e geometria dispostos na base nacional comum curricular. Vale ressaltar que para o sexto ano serão apresentados materiais apenas para os eixos de números e geometria para o oitavo ano somente para os eixos de números e álgebra.
Esta revisão bibliográfica será realizada mediante uma leitura sistemática, com a realização de fichamento de cada material pesquisado, de modo a ressaltar os pontos principais de cada obra que estejam enquadrados no tema desta pesquisa. As leituras serão executadas a domicílio e quando possível no polo de apoio presencial.
7. CONSIDERAÇÕES FINAIS
Refletindo sobre o objeto e problema desta pesquisa, pode-se ter uma conclusão de que o ensino de matemática pode se tornar mais agradável quando o professor utilizar em suas aulas materiais manipuláveis e/ou jogos, ou seja, os jogos, pois com estes além da aula se tornar descontraída, o aluno pode aprender melhor.
Em relação a nova base nacional comum curricular, pode-se destacar que esta veio com o intuito de melhorar de certa forma a rede publica de ensino brasileiro. Uma das coisas mais importantes desta base é que existem eixos temáticos a serem seguidos. Na área da matemática, que é o foco desta pesquisa estes eixos se dividem em números, álgebra, grandezas e medidas e probabilidade e estatística, mas os eixos que fizeram parte da pesquisa foram somente os que retratam a álgebra, a geometria e os números.
Com esta pesquisa pude entender sobre o quanto é importante trabalhar os jogos e os materiais manipuláveis nas aulas de matemática com os alunos das séries finais do ensino fundamental, ou seja, do sexto ao nono ano. Os jogos pesquisados para o ensino da disciplina de acordo com a BNCC me trouxeram uma enorme expectativa de que o ensino pode sim ser melhorado, pois se fizermos um link entre os eixos temáticos para os quais os jogos foram pesquisados e descritos neste trabalho as aulas de matemática podem se tornar mais alegres.
REFERÊNCIAS
BRASIL. Parâmetros Curriculares Nacionais: matemática, v.3. Disponível em: <http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf>. Acesso em: 28. Jun.2019.
BRASIL. Base nacional comum curricular. Disponível em: << http://basenacionalcomum.mec.gov.br/>>. Acesso em: 30. Ago.2018.
CASARIN, Helen de Castro e Samuel José. Pesquisa Científica: da teoria à pratica. Curitiba: Intersaberes, 2012.
FRANÇA, Luísa. Tudo que você precisa saber sobre a base nacional comum curricular. Disponível em: <<https://www.somospar.com.br/bncc-base-nacional-comum-curricular/>> . Acesso em: 27. set. 2018.
GÓES, Anderson Roges Teixeira e Heliza Colaço. Ensino da matemática: concepções, metodologias, tendências e organização do trabalho pedagógico. Curitiba: Intersaberes, 2015.
GROENWLAD, C.L et al. Utilizando curiosidades e jogos matemáticos em sala de aula. Disponível em: <<https://www.somatematica.com.br/artigos/a1/>>. Acesso em: 23 ago. 2018.
MARTINELLI, Liliam Maria Born e Paulo. Materiais concretos para o ensino de matemática nos anos finais do ensino fundamental. Curitiba: Intersaberes, 2016, 1ª ed.
MOREIRA, Denise Silva Costa e DIAS, Vanessa Moreira. A importância dos jogos e dos materiais concretos na resolução de problemas de contagem no ensino fundamental. Belo Horizonte, 2010.
RIBEIRO, F.D. Metodologia do ensino de matemática e física: Jogos e modelagem na educação matemática. Curitiba: Intersaberes, 2012.
MIGUEL, S. Jogos e atividades lúdicas no ensino da álgebra. Disponível em: lhttp://www.diaadiaeducacao.pr.gov.br/portals/cadernospde/pdebusca/producoes_pde/2014/2014_unioeste_mat_pdp_sirlei_miguel.pdf. Acesso em: 03 abr. 2019.
NEVES, E.A. Jogos matemáticos como recursos didáticos. Disponível em <https://meuartigo.brasilescola.uol.com.br/matematica/jogos-matematicos-como-rcursos-didaticos.htm> . Acesso em: 27.jun.2019.
OLIVEIRA, D.M. Jogos matemáticos otimizando o ensino de matemática no 8º ano do ensino fundamental. Disponível em: <http://www.diaadiaeducacao.pr.gov.br/portals/cadernospde/pdebusca/producoes_pde/2013/2013_unicentro_mat_pdp_debora_martins_de_oliveira.pdf>. Acesso em: 18. jan. 2019.
PERES, E.C. Jogos Matemáticos e Equação do Segundo Grau. Disponível em: <http://www.diaadiaeducacao.pr.gov.br/portals/cadernospde/pdebusca/producoes_pde/2014/2014_uem_mat_pdp_eliana_cristina_peres.pdf>. Acesso em: 26. out.2018
________ . Bingo de potências e raízes. Disponível em: < http://pibidmath.blogspot.com/2013/06/bingo-de-potencias-e-raizes.html>. Acesso em: 07. fev. 2019.
________ . Sugestões de jogos. Disponível em: <http://www.educacional.com.br/upload/blogSite/1012/1012548/22835/Programa%20de%20Cursos%202011%20%206%20ao%209%20ano%20JOGOS303201114553.pdf>. Acesso em: 10. fev.2019.
________ . Jogos de equações do 1º grau. Disponível em: <http://lemfafiuv.pbworks.com/w/file/fetch/107225556/Jogos%20Equa%C3%A7%C3%B5es%20de%201%C2%BA%20grau.pdf>. Acesso em: 23. dez.2018.





























