Resolução das inequações trigonométricas fundamentais
Quase todas as inequações trigonométricas, quando convenientemente tratadas e transformadas, podem ser reduzidas a pelo menos uma das inequações fundamentais. Vamos conhecê-las, a seguir, através de exemplos.
1º caso : sen x < sen a (sen x ![]() sen a)
sen a)
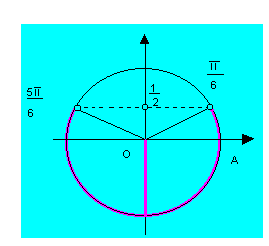
Por exemplo, ao resolvermos a inequação ![]() encontramos,
inicialmente,
encontramos,
inicialmente, ![]() ,
que
é uma solução particular no intervalo
,
que
é uma solução particular no intervalo ![]() .
Acrescentando
.
Acrescentando ![]() às extremidades dos intervalos encontrados, temos a solução geral em
IR, que é:
às extremidades dos intervalos encontrados, temos a solução geral em
IR, que é:
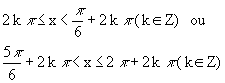
O conjunto solução é, portanto:
![]()
Por outro lado, se a inequação fosse ![]() , então, bastaria incluir as extremidades de
, então, bastaria incluir as extremidades de ![]() e o conjunto solução seria:
e o conjunto solução seria:
![]()
2º caso: sen x
> sen a (sen x ![]() sen
a)
sen
a)
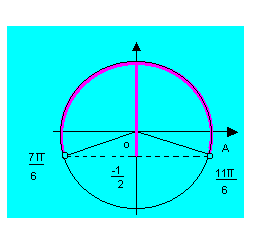
Acrescentando ![]()
![]() às extremidades
dos intervalos encontrados, temos a solução geral em IR, que é:
às extremidades
dos intervalos encontrados, temos a solução geral em IR, que é:
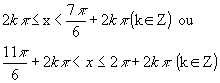
O conjunto solução é , portanto:
![]()
3º caso: cos x
< cos a (cos x ![]() cos
a)
cos
a)
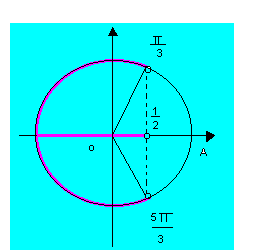
Acrescentando ![]() às extremidades do intervalo encontrado, temos a solução geral em IR, que é:
às extremidades do intervalo encontrado, temos a solução geral em IR, que é:
![]()
O conjunto solução é, portanto:
![]()
Por outro lado, se a inequação fosse cos x ![]() cos
cos ![]() ou cos x
ou cos x ![]() ,
então, bastaria incluir as extremidades de
,
então, bastaria incluir as extremidades de ![]() e o conjunto solução seria:
e o conjunto solução seria:
![]()





























