Você está em Ensino médio > Inequações trigonométricas ▼
Resolução das inequações trigonométricas fundamentais (parte 2)
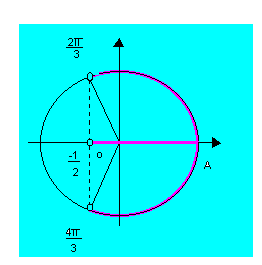
4º caso: cos x
> cos a (cos x 
cos
a)
encontramos,
inicialmente, 
,
que é uma solução particular no intervalo 
.
Acrescentando 
)
às extremidades dos intervalos encontrados, temos o conjunto
solução seguinte:
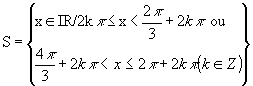
5º caso: tg x
< tg a (tg x 
tg a)
encontramos, inicialmente, 
,
que é uma solução particular no intervalo 
.
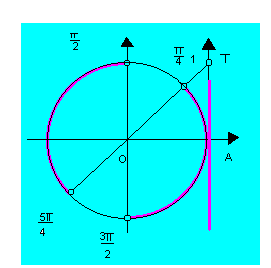
A solução geral em IR pode ser expressa
por 
.
O conjunto solução é, portanto:
6º caso: tg x > tg a ( tg x 
tg a)
Vamos estudar este último caso resolvendo a inequação tg x >
tg 
como exemplo.
encontramos, inicialmente,
,
que é uma solução particular no intervalo 
.
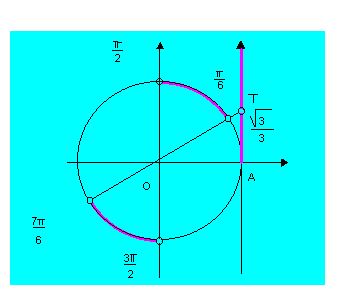
A solução geral em IR pode ser expressa por
.
O conjunto solução é, portanto:
Próximo conteúdo: Geometria analítica - Circunferência
Como referenciar: "Inequações trigonométricas" em Só Matemática. Virtuous Tecnologia da Informação, 1998-2025. Consultado em 07/03/2025 às 00:05. Disponível na Internet em https://www.somatematica.com.br/emedio/inequacoest/inequacoest3.php
