📄 Direção e sentido
📄 Segmentos equipolentes
📄 O que é um vetor?
📄 Alguns tipos de vetores
📄 Vetores colineares
📄 Vetores coplanares
📄 Operações com vetores
📄 Produto escalar
Produto escalar
Dados os vetores u=(a,b) e v=(c,d), definimos o produto escalar entre os vetores u e v, como o número real obtido por:
u.v = a.c + b.d
Exemplos:
O produto escalar entre u=(3,4) e v=(-2,5) é:
u.v = 3.(-2) + 4.(5) = -6+20 = 14
O produto escalar entre u=(1,7) e v=(2,-3) é:
u.v = 1.(2) + 7.(-3) = 2-21 = -19
Propriedades do produto escalar
Quaisquer que sejam os vetores, u v
e w e k escalar:
| v.w = w.v v.v = |v| |v| = |v|2 u.(v+w) = u.v + u.w (kv).w = v.(kw) = k(v.w) |kv| = |k| |v| |u.v| <= |u| |v| (desigualdade de Schwarz) |u+v| <= |u| + |v| (desigualdade triangular) Obs: <= significa menor ou igual |
Ângulo entre dois vetores
O produto escalar entre os vetores u e v pode ser escrito na forma:
u.v = |u| |v| cos(x)
onde x é o ângulo formado entre u e v.
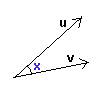
Através desta última definição de produto escalar, podemos obter o ângulo x entre dois vetores genéricos u e v, como:
![]()
desde que nenhum deles seja nulo.
Vetores ortogonais
Dois vetores u e v são ortogonais se:
u.v = 0




























