|
Ângulos
ÂNGULOS OPOSTOS PELO VÉRTICE
Observe os ângulos AÔB e CÔD na
figura abaixo:
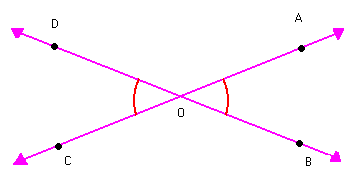
Verifique que:
Nesse caso, dizemos que os ângulos AÔB
e CÔD são opostos pelo vértice (o.p.v). Assim:
| Dois ângulos são
opostos pelo vértice quando os lados de um deles são semi-retas opostas
aos lados do outro. |
Na figura abaixo, vamos indicar:
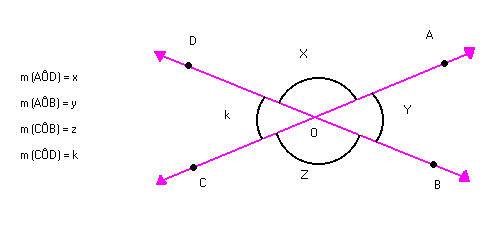
Sabemos que:
X + Y = 180º ( ângulos adjacentes suplementares)
X + K = 180º ( ângulos adjacentes suplementares)
Então:
Logo:
y = k
Assim:
m (AÔB) = m (CÔD)  AÔB
 CÔD
m (AÔD) = m (CÔB) AÔD
CÔB
Daí a propriedade:
|
Dois ângulos opostos pelo
vértice são congruentes.
|
Observe uma aplicação dessa propriedade na resolução
de um problema:
- Dois ângulos opostos pelo vértice têm medidas, em
graus, expressas por x + 60º e 3x - 40º. Qual é o valor de x?
Solução:
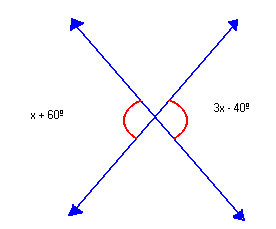
| x + 60º = 3x - 40º
ângulos
o.p.v
x -
3x = - 40º - 60º
-2x = - 100º
x = 50º
Logo, o valor de x é 50º. |
 |
<<
Voltar para seção Ensino fundamental
|
