Soma das medidas dos ângulos internos de um quadrilátero convexo

Podemos provar tal afirmação decompondo o quadrilátero ABCD nos triângulos ABD e BCD.

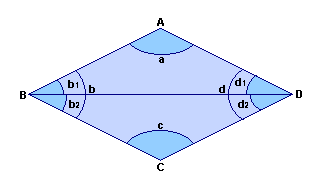
a + b₁ + d₁ = 180º.      (1)

Do triângulo BCD, temos:

c + b₂ + d₂ = 180º.       (2)

Adicionando (1) com (2), obtemos:

a + b₁ + d₁ + c + b₂ + d₂ = 180º + 180º
a + b₁ + d₁ + c + b₂ + d₂ = 360º

a + b + c + d = 360º

Observações:

1.Termos  uma fórmula geral para determinação da soma dos ângulos internos de qualquer polígono convexo:

2. A soma dos ângulos externos de um polígono convexo qualquer é 360º.