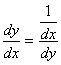Regra da cadeia

Com as regras que temos à nossa disposição até o presente momento, não conseguimos calcular alguns tipos de derivadas.

Veremos agora a regra da cadeia, uma fórmula para a derivada da função composta de duas funções. Criada por Gottfried Leibniz, a regra da cadeia teve grande importância para o avanço do cálculo diferencial. 

A fórmula é a seguinte:

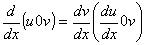
Ela pode ser escrita como: 

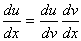
Outra fórmula similar é a seguinte:

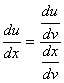
Exemplo

Calcular

Procedemos do seguinte modo:

Escrevemos y = ln (x² + 1). Com a esperança de usar a derivada de ln, faremos:

u = x² + 1
y = ln u

Calculamos:

Usamos a regra da cadeia, cujo primeiro membro é a derivada procurada:

ou seja, multiplicando as derivadas obtidas no passo anterior:

 Usamos agora a expressão de u que é (x² + 1), para obter

Derivada da função inversa

A inversa da função y(x) é a função x(y):