Propriedades do triângulo de Pascal

P1 - Em qualquer linha, dois números binomiais equidistantes dos extremos são iguais.

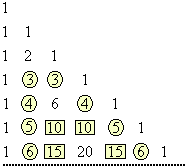
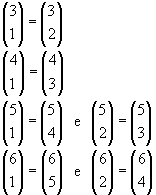
De fato, esses binomiais são complementares.

P2 - Teorema das linhas: a soma dos elementos da enésima linha é .

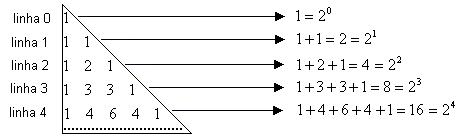
De modo geral temos:

P3 - Teorema das colunas: a soma dos elementos de qualquer coluna, do 1º elemento até um qualquer, é igual ao elemento situado na coluna à direita da considerada e na linha imediatamente abaixo.

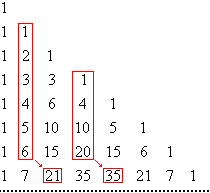
1 + 2 + 3 + 4 + 5 + 6 = 21

1 + 4 + 10 + 20 = 35

P4 - Teorema das diagonais: a soma dos elementos situados na mesma diagonal desde o elemento da 1ª coluna até o de uma qualquer é igual ao elemento imediatamente abaixo deste.

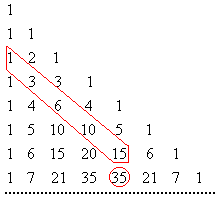
1 + 3 + 6 + 10 + 15 = 35