Função inversa

Consideremos os conjuntos A={0,2,4,6,8} e B={1,3,5,7,9} e a função f:AB definida por y=x+1. A função f está representada no diagrama abaixo:

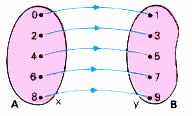
A função f é bijetora. A cada elemento x de A está associado um único elemento y de B, de modo que y=x+1. Porém, como f é bijetora, a cada elemento y de B está associado um único elemento x de A, de modo que x=y-1; portanto temos uma outra função g:BA, de modo que x=y-1 ou g(y)=y-1. Essa função está representada no diagrama abaixo:

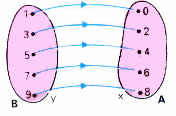
Pelo que acabamos de ver, a função f leva x até y, enquanto a função g leva y até x. A função g:BA recebe o nome de função inversa de f e é indicada por f^-1.

O domínio de f é o conjunto imagem de g, e o conjunto imagem de f é o domínio de g. Quando queremos, a partir da sentença y=f(x), obter a sentença de f^-1(x), devemos realizar os seguintes passos:

1º) Isolamos x na sentença y=f(x)
2º) Pelo fato de ser usual a letra x como símbolo da variável independente, trocamos x por y e y por x.

Por exemplo, para obter a função inversa de f:IRIR definida por y=2x+1, devemos:

1º) isolar x em y=2x+1. Assim y=2x+1 y-1=2x   x=(y-1)/2
2º) trocar x por y e y por x: y=(x-1)/2.

Portanto a função inversa de f é: f^-1(x)=(x-1)/2.

Observação: Para que uma função f admita a inversa f^-1 é necessário que ela seja bijetora. Se f não for bijetora, ela não possuirá inversa.

Exercício resolvido

* Esse conteúdo foi criado pelo Só Matemática. Os gráficos e diagramas foram retirados do livro Matemática - Volume Único. Ed.Saraiva.