Função par e função ímpar

Dada uma função f: AB, dizemos que f é par se, e somente se, f(x)=f(-x) para todo x A. Ou seja: os valores simétricos devem possuir a mesma imagem. O diagrama a seguir mostra um exemplo de função par:

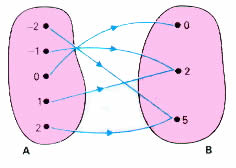
Por exemplo, a função f: IRIR definida por f(x)=x² é uma função par, pois f(x)=x²=(-x)²=f(-x). Podemos notar a paridade dessa função observando o seu gráfico:

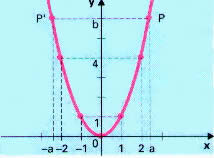
Notamos no gráfico que existe uma simetria em relação ao eixo vertical. Elementos simétricos têm a mesma imagem. Os elementos 2 e –2, por exemplo, são simétricos e possuem a imagem 4.

Por outro lado, dada uma função f: AB, dizemos que f é ímpar se, e somente se, f(-x)=-f(x) para todo x A. Ou seja: valores simétricos possuem imagens simétricas. O diagrama a seguir mostra um exemplo de função ímpar:

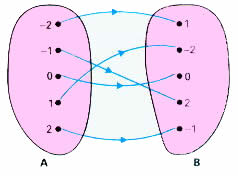
Por exemplo, a função f: IRIR definida por f(x)=x³ é uma função ímpar, pois f(-x)=(-x)³=-x³=-f(x). Podemos notar que a função é ímpar observando o seu gráfico:

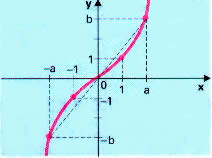
Notamos no gráfico que existe uma simetria em relação a origem 0. Elementos simétricos têm imagens simétricas. Os elementos 1 e –1, por exemplo, são simétricos e possuem imagens 1 e –1 (que também são simétricas).

Obs: Uma função que não é par nem ímpar é chamada função sem paridade.

Exercício resolvido:

Classifique as funções abaixo em pares, ímpares ou sem paridade:

a) f(x)=2x
f(-x)= 2(-x) = -2x f(-x) = -f(x), portanto f é ímpar.

b) f(x)=x²-1
f(-x)= (-x)²-1 = x²-1 f(x)=f(-x), portanto f é par.

c) f(x)=x²-5x+6
f(-x)= (-x)²-5(-x)+6 = x²+5x+6
Como f(x)f(-x), então f não é par.
Temos também que –f(x)f(-x), logo f não é ímpar.
Por não ser par nem ímpar, concluímos que f é função sem paridade.