📄 Domínio e imagem de uma função
📄 Obtenção do domínio
📄 Construção do gráfico cartesiano
📄 Raízes de uma função
📄 Propriedades de uma função
📄 Função par e função ímpar
📄 Funções crescente e decrescente
📄 Função composta
📄 Função inversa
Domínio e imagem de uma função
O domínio de uma função de A em B é sempre o próprio conjunto de partida, ou seja, D=A. Se um elemento x 
A estiver associado a um elemento y B, dizemos que y é a imagem de x (indica-se y=f(x) e lê-se “y é igual a f de x”).
Observe o domínio e a imagem na função abaixo.
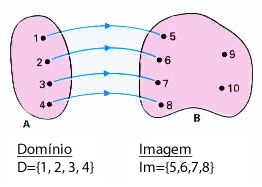
Outro exemplo: se f é uma função de IN em IN (isto significa que o domínio e o contradomínio são os números naturais) definida por y=x+2, então temos que:
- A imagem de 1 através de f é 3, ou seja, f(1)=1+2=3;
- A imagem de 2 através de f é 4, ou seja, f(2)=2+2=4;
De modo geral, a imagem de x através de f é x+2, ou seja: f(x)=x+2.
Em uma função f de A em B, os elementos de B que são imagens dos elementos de A através da aplicação de f formam o conjunto imagem de f. Segundo o conceito de função, existem duas condições para que uma relação f seja uma função:
Observações:
- Como x e y têm seus valores variando nos conjuntos A e B, recebem o nome de variáveis.
- A variável x é chamada variável independente e a variável y, variável dependente, pois para obter o valor de y dependemos de um valor de x.
- Uma função f fica definida quando são dados seu domínio (conjunto A), seu contradomínio (conjunto B) e a lei de associação y=f(x).
Exercícios resolvidos
1) Considere a função f: A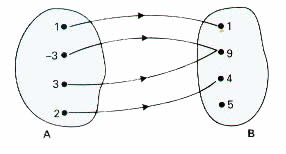
B representada pelo diagrama a seguir:
Determine:
b) f(1), f(-3), f(3) e f(2);
c) o conjunto imagem (Im) de f;
d) a lei de associação
Resolução:
a) O domínio é igual ao conjunto de partida, ou seja, D=A.b) f(1)=1, f(-3)=9, f(3)=9 e f(2)=4.
c) O conjunto imagem é formado por todas imagens dos elementos do domínio, portanto:
Im = {1,4,9}.
d) Como 12=1, (-3)2=9, 32=9 e 22=4, temos y=x2.
2) Dada a função f: IRIR (ou seja, o domínio e a contradomínio são os números reais) definida por f(x)=x2-5x+6, calcule:
a) f(2), f(3) e f(0);
b) o valor de x cuja imagem vale 2.
Resolução:
a) f(2)= 22-5(2)+6 = 4-10+6 = 0f(3)= 32-5(3)+6 = 9-15+6 = 0
f(0)= 02-5(0)+6 = 0-0+6 = 6
b) Calcular o valor de x cuja imagem vale 2 equivale a resolver a equação f(x)=2, ou seja, x2-5x+6=2. Utilizando a fórmula de Bhaskara encontramos as raízes 1 e 4. Portanto os valores de x que têm imagem 2 são 1 e 4.
