Circunferência

Circunferência é o conjunto de todos os pontos de um plano equidistantes de um ponto fixo desse mesmo plano, denominado centro da circunferência:

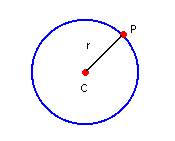
Equações da circunferência

Equação reduzida

Sendo C(a, b) o centro e P(x, y) um ponto qualquer da circunferência, a distância de C a P(d_CP) é o raio dessa circunferência. Então:

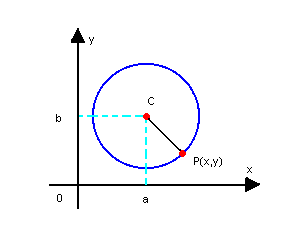
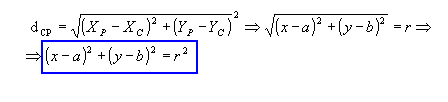
Portanto, (x - a)² + (y - b)² =r² é a equação reduzida da circunferência e permite determinar os elementos essenciais para a construção da circunferência: as coordenadas do centro e o raio.

Observação: Quando o centro da circunferência estiver na origem (C(0,0)), a equação da circunferência será x² + y² = r².

Equação geral

Desenvolvendo a equação reduzida, obtemos a equação geral da circunferência:

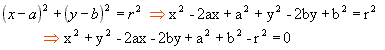
Como exemplo, vamos determinar a equação geral da circunferência de centro C(2, -3) e raio r = 4.

A equação reduzida da circunferência é:

(x - 2)²  + (y + 3)² = 16

Desenvolvendo os quadrados dos binômios, temos: