Matrizes

Introdução

O crescente uso dos computadores tem feito com que a teoria das matrizes seja cada vez mais aplicada em áreas como Economia, Engenharia, Matemática, Física, dentre outras. Vejamos um exemplo. A tabela a seguir representa as notas de três alunos em uma etapa:

Se quisermos saber a nota do aluno B em Literatura, basta procurar o número que fica na segunda linha e na terceira coluna da tabela.

Vamos agora considerar uma tabela de números  dispostos em linhas e colunas, como no exemplo acima, mas colocados entre parênteses ou colchetes:

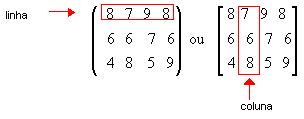
Em tabelas assim dispostas, os números são os elementos. As linhas são enumeradas de cima para baixo e as colunas, da esquerda para direita:

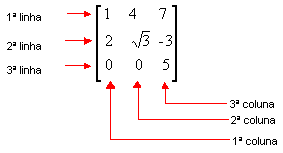
Tabelas com m linhas e n colunas (m e n números naturais diferentes de 0) são denominadas matrizes m x n. Na tabela anterior temos, portanto, uma matriz 3 x 3. Veja mais alguns exemplos:

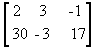• é uma matriz do tipo 2 x 3

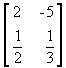• é uma matriz do tipo 2 x 2