Matriz transposta, matriz simétrica e matriz oposta

• Matriz transposta: matriz A^t obtida a partir da matriz A trocando-se ordenadamente as linhas por colunas ou as colunas por linhas. Por exemplo:

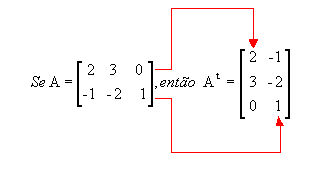
Desse modo, se a matriz A é do tipo m x n, A^t é do tipo n x m. Note que a 1ª linha de A corresponde à 1ª coluna de A^t e a 2ª linha de A corresponde à 2ª coluna de A^t.

• Matriz simétrica: matriz quadrada de ordem n tal que A = A^t . Por exemplo,

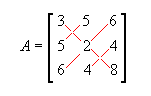é simétrica, pois a₁₂ = a₂₁ = 5, a₁₃ = a₃₁ = 6, a₂₃ = a₃₂ = 4, ou seja, temos sempre       a _ij = a _ji.
   

• Matriz oposta: matriz -A obtida a partir de A trocando-se o sinal de todos os elementos de A. Por exemplo, .

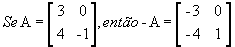Igualdade de matrizes

Duas matrizes, A e B, do mesmo tipo m x n, são iguais se, e somente se, todos os elementos que ocupam a mesma posição são iguais:

.