Sistemas equivalentes

Dois sistemas são equivalentes quando possuem o mesmo conjunto solução. Por exemplo, dados os sistemas:

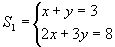          e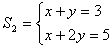   

verificamos que o par ordenado (x, y) = (1, 2) satisfaz ambos e é único. Logo, S₁ e S₂ são equivalentes: S₁ ~ S_2.

Propriedades

a) Trocando de posição as equações de um sistema, obtemos outro sistema equivalente. Por exemplo:

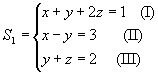e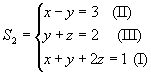   

S₁ ~ S₂

   
b) Multiplicando uma ou mais equações de um sistema por um número K (K IR*), obtemos um sistema equivalente ao anterior. Por exemplo:

S₁ ~ S₂

c) Adicionando a uma das equações de um sistema o produto de outra equação desse mesmo sistema por um número k ( K IR*), obtemos um sistema equivalente ao anterior.

Por exemplo:

Dado 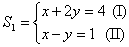 , substituindo a equação (II) pela soma do produto de (I) por -1 com (II), obtemos:

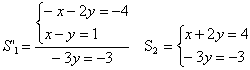
S₁~S₂, pois (x,y)=(2,1) é solução de ambos os sistemas.