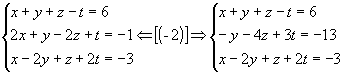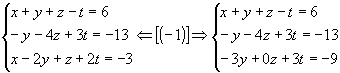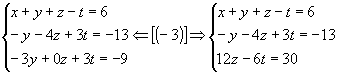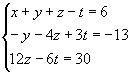Sistemas escalonados (continuação)

II) O número de equações é menor que o número de incógnitas (m < n)

Exemplo: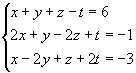

1º passo: Anulamos todos os coeficientes da 1ª incógnita a partir da 2ª equação:

2º passo: Anulamos os coeficientes da 2ª incógnita, a partir da 3ª equação:

O sistema está escalonado. Como m<n, o sistema é possível e indeterminado, admitindo infinitas soluções. A diferença entre o número de incógnitas (n) e o de equações (m) de um sistema nessas condições é chamada grau de indeterminação (GI):

GI= n - m

Para resolver um sistema indeterminado, procedemos do seguinte modo:

Como o grau de indeterminação é 1, atribuímos a uma das incógnitas um valor , supostamente conhecido, e resolvemos o sistema em função desse valor. Sendo t=, substituindo esse valor na 3ª equação, obtemos:

12z - 6= 3012z= 30 + 6 =

Conhecidos z e t, substituímos esses valores na 2ª equação:

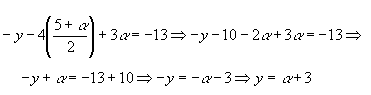
Conhecidos z,t e y, substituímos esses valores na 1ª equação:

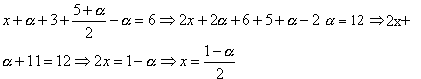
Assim, a solução do sistema é dada por S=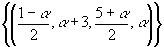, com IR.

Para cada valor que seja atribuído a , encontraremos uma quádrupla que é solução para o sistema.