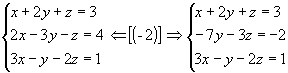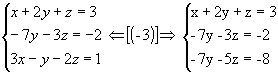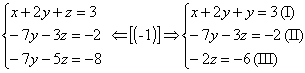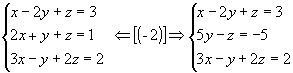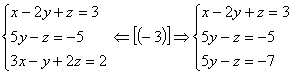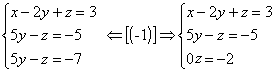Sistemas escalonados

Utilizamos a regra de Cramer para discutir e resolver sistemas lineares em que o número de equações (m) é igual ao número de incógnitas (n). Quando m e n são maiores que três, torna-se muito trabalhoso utilizar essa regra. Por isso, usamos a técnica do escalonamento, que facilita a discussão e resolução de quaisquer sistemas lineares.

Dizemos que um sistema, em que existe pelo menos um coeficiente não-nulo em cada equação, está escalonado se o número de coeficientes nulos antes do primeiro coeficiente não nulo aumenta de equação para equação. Para escalonar um sistema adotamos o seguinte procedimento:

a) Fixamos como 1ª equação uma das que possuem o coeficiente da 1ª incógnita diferente de zero.

b) Utilizando as propriedades de sistemas equivalentes, anulamos todos os coeficientes da 1ª incógnita das demais equações.

c) Repetimos o processo com as demais incógnitas, até que o sistema se torne escalonado.

Vamos então aplicar a técnica do escalonamento, considerando dois tipos de sistema:

I. O número de equações é igual ao número de incógnitas (m=n)

Exemplo 1:  

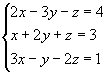
1ºpasso: Anulamos todos os coeficientes da 1ª incógnita a partir da 2ª equação, aplicando as propriedades dos sistemas equivalentes:

2º passo: Anulamos os coeficientes da 2ª incógnita a partir da 3ª equação:

Agora o sistema está escalonado e podemos resolvê-lo.

-2z=-6 z=3

Substituindo z=3 em (II):

-7y - 3(3)= -2 -7y - 9 = -2 y=-1

Substituindo z=3 e y=-1 em (I):

x + 2(-1) + 3= 3 x=2

Então, x=2, y=-1 e z=3

Exemplo 2: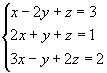  

1º passo: Anulamos todos os coeficientes da 1ª incógnita a partir da 2ª equação:

2º passo: Anulamos os coeficientes da 2ª incógnita, a partir da 3ª equação:

Dessa forma, o sistema está escalonando. Como não existe valor real de z tal que 0z=-2, o sistema é impossível.