Posição de um ponto em relação a uma circunferência

Em relação à circunferência de equação:

(x - a)² + (y - b)² = r²

O ponto P(m, n) pode ocupar as seguintes posições:

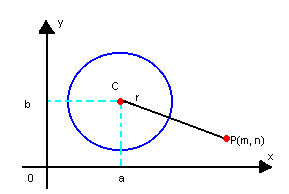
a) P é exterior à circunferência

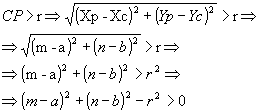
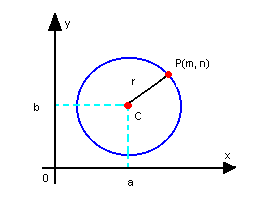
b) P pertence à circunferência

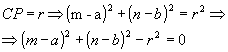
c) P é interior à circunferência

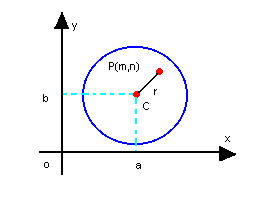
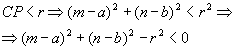
Assim, para determinar a posição de um ponto P(m, n) em relação a uma circunferência, basta substituir as coordenadas de P na expressão (x - a)² + (y - b)² - r²:

• se (m - a)² + (n - b)² - r² > 0, então P é exterior à circunferência;
• se (m - a)² + (n - b)² - r² = 0, então P pertence à circunferência;
• se (m - a)² + (n - b)² - r² < 0, então P é interior à circunferência.