Elipse

Considerando, num plano , dois pontos distintos, F₁ e F₂ e, sendo 2a um número real maior que a distância entre F₁ e F₂, chamamos de elipse o conjunto dos pontos do plano tais que a soma das distâncias desses pontos a F₁ e F₂ seja sempre igual a 2a.

Por exemplo, sendo P, Q, R, S, F₁ e F₂ pontos de um mesmo plano e F₁F₂ < 2a, temos:

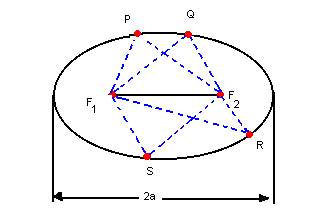
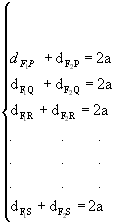
A figura obtida é uma elipse. Observações:

1ª) A Terra descreve uma trajetória elíptica em torno do sol, que é um dos focos dessa trajetória. A lua em torno da terra e os demais satélites em relação a seus respectivos planetas também apresentam esse comportamento.

2ª) O cometa de Halley segue uma órbita elíptica, tendo o Sol como um dos focos.

3ª) As elipses são chamadas cônicas porque ficam configuradas pelo corte feito em um cone circular reto por um plano oblíquo em relação à sua base.

Elementos

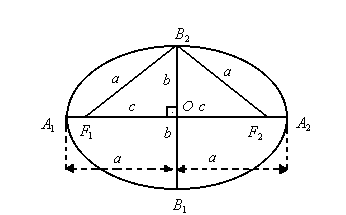
Observe a elipse a seguir. Nela, consideramos os seguintes elementos:

• focos : os pontos F₁ e F₂ 

• centro: o ponto O, que é o ponto médio de

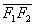
• semi-eixo maior: a

• semi-eixo menor: b

• semidistância focal: c

• vértices: os pontos A₁, A₂, B₁, B₂

• eixo maior:

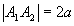
• eixo menor:

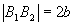
• distância focal:

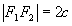
Relação fundamental

Na figura acima, aplicando o Teorema de Pitágoras ao triângulo OF₂B₂ , retângulo em O, podemos escrever a seguinte relação fundamental:

Excentricidade

Chamamos de excentricidade o número real e tal que:

Pela definição de elipse, 2c < 2a, então c < a e, consequentemente, 0 < e < 1.

Observação: quando os focos são muito próximos, ou seja, c é muito pequeno, a elipse se aproxima de uma circunferência.