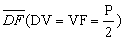Parábola

Dados uma reta d e um ponto F , de um plano , chamamos de parábola o conjunto de pontos do plano equidistantes de F e d.

Por exemplo, sendo F, P, Q e R pontos de um plano e d uma reta desse mesmo plano, de modo que nenhum ponto pertença a d, temos:

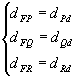
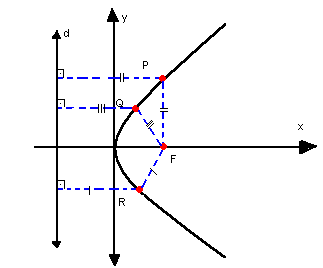
Observações:

1ª) A parábola é obtida seccionando-se obliquamente um cone circular reto:

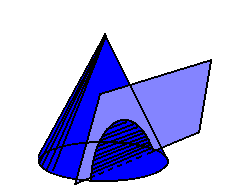
2ª) Os telescópios refletores mais simples têm espelhos com secções planas parabólicas.

3ª) As trajetórias de alguns cometas são parábolas, sendo que o Sol ocupa o foco.

4ª) A superfície de um líquido contido em um cilindro que gira em torno de seu eixo com velocidade constante é parabólica.

Elementos

Observe a parábola representada a seguir. Nela, temos os seguintes elementos:

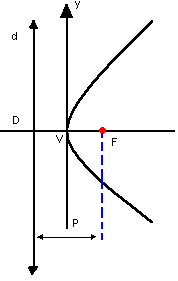
• foco: o ponto F

• diretriz: a reta d

• vértice: o ponto V

• parâmetro: p

                Então, temos que:

• o vértice V e o foco F ficam numa mesma reta, o eixo de simetria e.

                Assim, sempre temos .

• DF =p

• V é o ponto médio de