Hipérbole

Considerando, num plano , dois pontos distintos, F₁ e F₂ e, sendo 2a um número real menor que a distância entre F₁ e F₂, chamamos de hipérbole o conjunto dos pontos do plano tais que o módulo da diferença das distâncias desses pontos a F₁ e F₂ seja sempre igual a 2a.

Por exemplo, sendo P, Q, R, S, F1 e F2 pontos de um mesmo plano e F₁F₂ = 2c, temos:

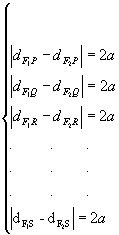
A figura obtida é uma hipérbole.

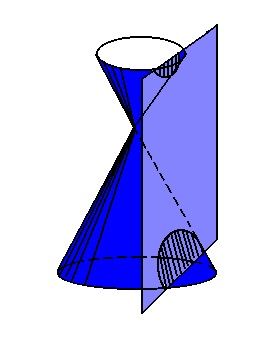
Observação: os dois ramos da hipérbole são determinados por um plano paralelo ao eixo de simetria de dois cones circulares retos e opostos pelo vértice:

Elementos

Observe a hipérbole representada a seguir. Nela, temos os seguintes elementos:

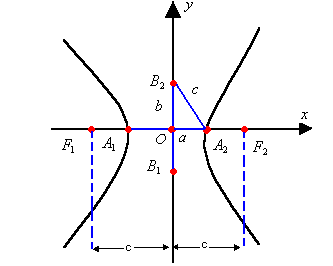
• focos: os pontos F₁ e F₂

• vértices: os pontos A₁ e A₂

• centro da hipérbole: o ponto O, que é o ponto médio de

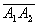
• semi-eixo real: a

• semi-eixo imaginário: b

• semidistância focal: c

• distância focal:

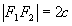
• eixo real:

• eixo imaginário:

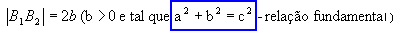
Excentricidade

Chamamos de excentricidade o número real e tal que:

Como c > a, temos e > 1.