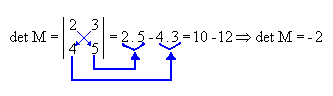|
Determinantes
Como já
vimos, matriz quadrada é a que tem o mesmo número de linhas e de colunas (ou
seja, é do tipo nxn).
A toda matriz
quadrada está associado um número ao qual damos o nome de determinante.
Dentre as
várias aplicações dos determinantes na Matemática, temos:
-
resolução de alguns
tipos de sistemas de equações lineares;
-
cálculo da área de um
triângulo situado no plano cartesiano, quando são conhecidas as
coordenadas dos seus vértices;
Determinante de
1ª ordem
Dada uma matriz
quadrada de 1ª ordem M=[a11], o seu determinante é o número real a11:
det M =Ia11I = a11
Observação: Representamos o
determinante de uma matriz entre duas barras verticais, que não têm o
significado de módulo.
Por exemplo:
- M= [5]
 det
M = 5 ou I 5 I = 5
|
- M = [-3] det
M = -3 ou I -3 I = -3
|
Determinante de 2ª ordem
Dada a matriz  ,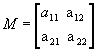
de ordem 2, por definição o determinante associado a M, determinante de
2ª ordem, é dado por:
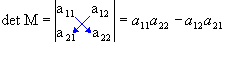
Portanto, o determinante
de uma matriz de ordem 2 é dado pela diferença entre o produto dos elementos
da diagonal principal e o produto dos elementos da diagonal secundária. Veja o
exemplo a seguir.
Menor
complementar
Chamamos de menor
complementar relativo a um elemento aij de uma
matriz M, quadrada e de ordem n>1, o determinante MCij ,
de ordem n - 1, associado à matriz obtida de M quando suprimimos a linha
e a coluna que passam por aij .
Vejamos como
determiná-lo pelos exemplos a seguir:
a) Dada a matriz ,
de ordem 2, para determinar o menor complementar relativo ao elemento a11(MC11),
retiramos a linha 1 e a coluna 1:
Da mesma forma, o menor complementar relativo
ao elemento a12 é:
b) Sendo  ,
de ordem 3, temos:
<<
Voltar para seção Ensino médio
|
