Determinantes

Regra de Sarrus

   O cálculo do determinante de 3ª ordem pode ser feito por meio de um dispositivo prático, denominado regra de Sarrus.

   Acompanhe como aplicamos essa regra para .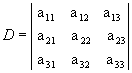

1º passo: Repetimos as duas primeiras colunas ao lado da terceira:

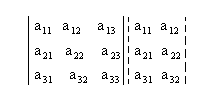
2º passo: Encontramos a soma do produto dos elementos da diagonal principal com os dois produtos obtidos pela multiplicação dos elementos das paralelas a essa diagonal (a soma deve ser precedida do sinal positivo):

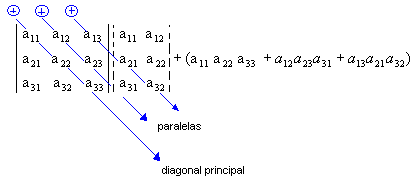
3º passo: Encontramos a soma do produto dos elementos da diagonal secundária com os dois produtos obtidos pela multiplicação dos elementos das paralelas a essa diagonal ( a soma deve ser precedida do sinal negativo):

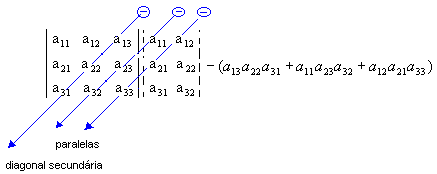
Assim:

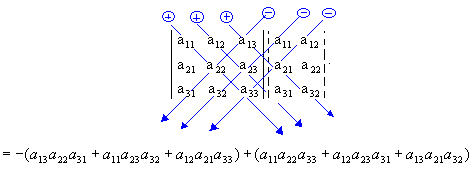
Observação: Se desenvolvermos esse determinante de 3ª ordem aplicando o Teorema de Laplace, encontraremos o mesmo número real.

Determinante de ordem n > 3

   Vimos que a regra de Sarrus é válida para o cálculo do determinante de uma matriz de ordem 3. Quando a matriz é de ordem superior a 3, devemos empregar o Teorema de Laplace para chegar a determinantes de ordem 3 e depois aplicar a regra de Sarrus.

<< Voltar para seção Ensino médio