Você está em Ensino médio > Determinantes ▼
📄 Introdução
📄 Menor complementar
📄 Cofator
📄 Teorema de Laplace
📄 Regra de Sarrus
📄 Propriedades dos determinantes
📄 Propriedades (parte 2)
📄 Propriedades (parte 3)
📄 Menor complementar
📄 Cofator
📄 Teorema de Laplace
📄 Regra de Sarrus
📄 Propriedades dos determinantes
📄 Propriedades (parte 2)
📄 Propriedades (parte 3)
Cofator
Chamamos de cofator ou complemento algébrico relativo a um elemento aij de uma matriz quadrada de ordem n o número Aij tal que Aij = (-1)i+j . MCij .
Acompanhe o exemplo:
a) Dada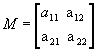 
,
os cofatores relativos aos elementos a11 e a12 da
matriz M são:
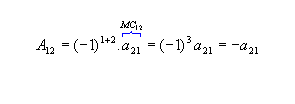
b) Sendo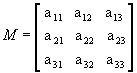 
,
vamos calcular os cofatores A22, A23 e A31:
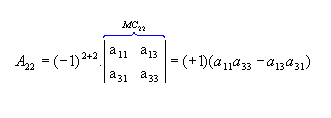
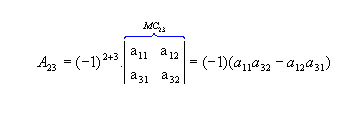
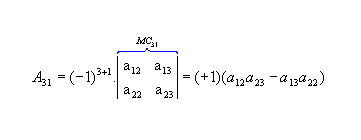
Próximo: Teorema de Laplace
Como referenciar: "Determinantes" em Só Matemática. Virtuous Tecnologia da Informação, 1998-2025. Consultado em 02/04/2025 às 03:32. Disponível na Internet em https://www.somatematica.com.br/emedio/determinantes/determinantes2.php
