Teorema de Laplace

O determinante de uma matriz quadrada M = [a_ij]_mxn pode ser obtido pela soma dos produtos dos elementos de uma fila qualquer (linha ou coluna) da matriz M pelos respectivos cofatores.

Assim, fixando , temos:

em que é o somatório de todos os termos de índice i, variando de 1 até m, .

Exemplo:

Calcule o determinante da matriz A, aplicando o Teorema de Laplace:

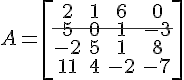
Destacando a segunda linha da matriz, temos D = 5 . A₂₁ + 0 . A₂₂ + 1 . A₂₃ + (-3) . A₂₄. Vamos calcular os cofatores:

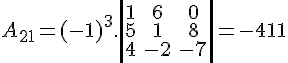
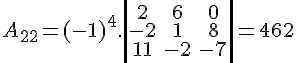
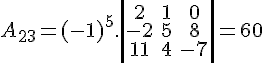
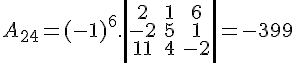
Para finalizar, calculamos o determinante:

D = 5 . A₂₁ + 0 . A₂₂ + 1 . A₂₃ + 3 . A₂₄
D = 5 . (–411) + 0 . (462) + 1 . (60) + (–3) . (–399)
D = –2055 + 0 + 60 + 1197
D = – 798