Divisão de um polinômio por (x – a)(x – b)

Vamos supor que um polinômio P(x) é divisível por (x – a) e por (x –b), sendo ab . Será que P(x) é divisível pelo produto (x – a)(x – b)?

O divisor (x – a)(x – b) tem grau 2, logo o resto terá, no máximo, grau 1.

Então, podemos escrever:

Como P(x) é divisível por (x – a), então P(a) = 0:

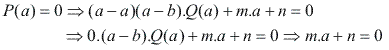
Como P(x) é divisível por (x –b), então P(b) = 0:

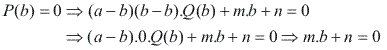
Temos o seguinte sistema de equações:

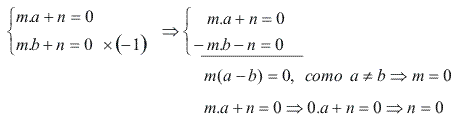
Portanto, podemos concluir que P(x) é divisível por (x – a)(x – b).

Temos, deste modo, o seguinte teorema:

Se P(x) é divisível por (x – a) e por (x – b) com ab, então P(x) é divisível por (x – a)(x – b).

Generalizando o teorema, se P(x) é divisível por com  distintos, então P(x) é divisível por .

Exemplo 1

O polinômio  é divisível por (x - 1)(x - 2)?

Resolução

Se P(x) for divisível por (x - 1) e por (x - 2), então P(x) será divisível por (x - 1)(x - 2).

P(x) é divisível por (x -1), isto é, P(1) = 0?

 - Sim.

P(x) é divisível por (x - 2), isto é, P(2) = 0?

- Sim.

Como P(x) é divisível por (x -1) e por (x - 2) então P(x) é divisível por (x - 1)(x - 2).

Exemplo 2

Um polinômio P(x), dividido por x – 1, dá resto 4; dividido por x +1, dá resto 2. Qual o resto da divisão de P(x) por (x – 1)(x + 1)?

Resolução

Como o divisor (x – 1)(x + 1) tem grau 2, o grau do resto será no máximo 1. Podemos escrever:

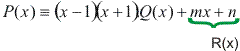
P(x) dividido por x – 1 dá resto 4. Assim, P(1) = 4:

P(x) dividido por x + 1 dá resto2. Assim, P(-1) = 2:

Temos o seguinte sistema de equações:

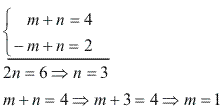
Portanto, o resto da divisão de P(x) por (x – 1)(x + 1) é x + 3.