Laifis em destaque

Raças de Gatos 66 postagens Meio Ambiente 33 postagens

Fusca-Aranha! 15 assustadoras esculturas 26 postagens Maquiagens para todas ocasiões 72 postagens

 COMPOSIÇÃO DE UMA EQUAÇÃO DO 2º GRAU, CONHECIDAS AS RAÍZES

 Considere a equação do 2º grau ax² + bx + c = 0.

 Dividindo todos os termos por a , obtemos:

Como , podemos escrever a equação desta maneira.

Exemplos:

• Componha a equação do 2º grau cujas raízes são -2 e 7.

Solução

A soma das raízes corresponde a:

S= x₁ + x₂ = -2 + 7 = 5

O produto das raízes corresponde a:

P= x₁ . x₂ = ( -2) . 7 = -14

A equação do 2º grau é dada por x² - Sx + P = 0, onde S=5 e P= -14.

Logo, x² - 5x - 14 = 0 é a equação procurada.

• Formar a equação do 2º grau, de coeficientes racionais, sabendo-se que uma das raízes é  .

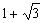Solução

Se uma equação do 2º grau, de coeficientes racionais, tem uma raiz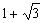  , a outra raíz será  .

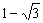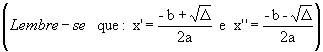
    Assim:

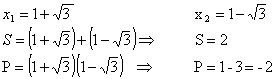
Logo, x² - 2x - 2 = 0 é a equação procurada.

 FORMA FATORADA

 Considere a equação ax² + bx + c = 0.

 Colocando a em evidência, obtemos:

Então, podemos escrever:

Logo, a forma fatorada da equação ax² + bx + c = 0 é:

Exemplos:

• Escreva na forma fatorada a equação x² - 5x + 6 = 0.

Solução

Calculando as raízes da equação x² - 5x + 6 = 0, obtemos x₁= 2 e x₂= 3.

Sendo a= 1, x₁= 2 e x₂= 3, a forma fatorada de x² - 5x + 6 = 0 pode ser assim escrita:

(x-2).(x-3) = 0

• Escreva na forma fatorada a equação 2x² - 20x + 50 = 0.
     

Solução

Calculando as raízes da equação 2x² - 20x + 50 = 0, obtemos duas raízes reais e iguais a 5.

Sendo a= 2, x₁=x₂= 5, a forma fatorada de 2x² - 20x + 50 = 0 pode ser assim escrita:

2.(x - 5) (x - 5) = 0  ou 2. (x - 5)²=0

• Escreva na forma fatorada a equação x² + 2x + 2 = 0.

Solução

Como o , a equação não possui raízes reais.

Logo, essa equação não possui forma fatorada em IR.

<< Voltar para seção Ensino fundamental