Composição da equação biquadrada

Toda equação biquadrada de raízes reais x₁, x₂, x₃ e x₄ pode ser composta pela fórmula:

Exemplo:

• Compor a equação biquadrada cujas raízes são:
   
  Solução:
  

  a) (x - 0) (x - 0) (x + 7) (x - 7) = 0       x2(x2 -49) = 0     x4 - 49x2 = 0

  b) (x + a) (x - a) (x + b) (x - b) = 0     (x2-a2) (x2-b2) = 0     x4 - (a2 + b2) x2 + a2b2 = 0

Propriedades das raízes da da equação biquadrada

Consideremos a equação ax⁴ + bx² + c = 0, cujas raízes são x₁, x₂, x₃ e x₄ e a equação do 2º grau ay² + by + c = 0, cujas raízes são y' e y''.De cada raiz da equação do 2º grau, obtemos duas raízes simétricas para a biquadrada. Assim:

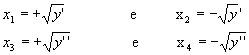
Do exposto, podemos estabelecer as seguintes propriedades:

1ª propriedade: a soma das raízes reais da equação biquadrada é nula.

2ª propriedade: a soma dos quadrados das raízes reais da equação biquadrada é igual a -.

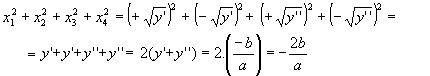
3ª propriedade: o produto das raízes reais e não-nulas da equação biquadrada é igual a .