Outros exemplos de problemas do 2º grau

• Duas torneiras enchem um tanque em 6 horas. Sozinha, uma delas gasta 5 horas mais que a outra. Determine o tempo que uma delas leva para encher esse tanque isoladamente.
  Solução:
  Consideremos x o tempo gasto para a 1ª torneira encher o tanque e x+5 o tempo gasto para a 2ª torneira encher o tanque.
  
  Em uma hora, cada torneira enche a seguinte fração do tanque:
  
  Em uma hora, as duas torneiras juntas encherão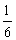 do tanque; observe a equação correspondente:
  
  Resolvendo-a, temos:
  6( x + 5 ) + 6x = x ( x + 5 )
  6x + 30 + 6x = x² + 5x
  x² - 7x - 30 = 0
  x'= - 3      e   x''=10
  
  Como a raiz negativa não é utilizada, teremos como solução x= 10.
  Resposta: A 1ª torneira enche o tanque em 10 horas e a 2ª torneira, em 15 horas.

• Num jantar de confraternização, seria distribuído, em partes iguais, um prêmio de R$ 24.000,00 entre os convidados. Como faltaram 5 pessoas, cada um dos presentes recebeu um acréscimo de R$ 400,00 no seu prêmio. Quantos pessoas estavam presentes nesse jantar?
  Solução:
  Podemos representar por:
  
  Resolvendo-a:
  
  Resposta:  Nesse jantar deveriam estar presentes 20 pessoas. Como faltaram 5, então 15 pessoas estavam presentes no jantar.