Série-P, série alternada e série de potência

Série-P

É uma série da seguinte forma:

CONVERGE se p > 1
DIVERGE se p1

Se p = 1, a série

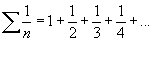é chamada série harmônica e, de acordo com o teorema, é divergente.

Série alternada

É da forma:

Séries de potência

Séries de potências de x

ou

Séries de potência de (x-c)

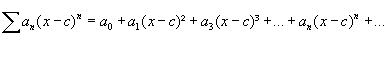
Por conveniência, vamos admitir que , mesmo quando x = 0.

Ao substituir x por um número real, obtém-se uma série de termos constantes que pode convergir ou divergir.

Em qualquer série de potências de x, a série converge sempre para x=0, pois se substituirmos x por 0 a série se reduz a a₀.

Na série de potências de (x-c), a série converge para x = c.

Para determinar os outros valores de x para os quais a série converge, utiliza-se o teste da razão.