Números complexos

Vamos considerar a equação x² - 2x + 5 = 0:

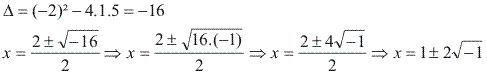
Sabemos que o número não pertence ao conjunto dos números reais, pois não existe nenhum número que elevado ao quadrado resulte em -1. Para que a equação acima tenha solução, temos que estender o conjunto dos números reais para obter um novo conjunto, chamado de conjunto dos números complexos e representado por .
O número  foi denominado unidade imaginária e criou-se o número i, de modo que:

Logo,

i =

Portanto, as soluções da equação x² - 2x + 5 = 0 em  são 1 - 2i e 1 + 2i.

Forma algébrica de um número complexo

Todo número complexo z pode ser escrito na forma:

z =  a + bi, com a, b

Essa forma é chamada forma algébrica do número complexo. Observe que um número complexo nesse formato tem duas partes:

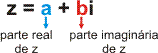
Indicamos:
Re(z) = a
Im(z) = b

Exemplos

• z =  3 + 5i             Re(z) = 3 e Im(z) = 5
• z = -7 +18i            Re(z) = -7 e Im(z) = 18
• z = 53 – 25i          Re(z) = 53 e Im(z) = -25

• Se a parte real do número complexo é nula, então o número é imaginário puro.

Exemplo: z = 3i    Re(z) = 0 e Im(z) = 3

Exemplo

Determine o valor de k para que o número complexo z = (k – 4) +3i seja imaginário puro:

Resolução
Para que o número seja imaginário puro, a parte real deve ser nula:

k – 4 = 0  k = 4

• Se a parte imaginária do número complexo é nula, então o número é real.

Exemplo: z = 10   Re(z) = 10 e Im(z) = 0

Exemplo

Determine o valor de k para que o número complexo z = 3+(k² – 4)i seja um número real:

Resolução
Para que o número seja real, a parte imaginária deve ser nula:

k² – 4 = 0  k² = 4 k = -2 ou k = 2

Podemos associar  qualquer número complexo z = a +bi a um ponto no plano de Argand-Gauss. No eixo das abscissas (eixo real,) representa-se a parte real, e, no eixo das ordenadas (eixo imaginário), a parte imáginária do número complexo. O ponto P é o afixo ou imagem geométrica de z.

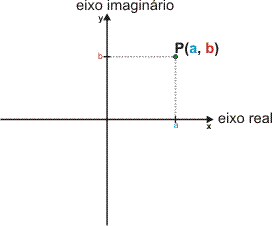
Exemplo

Represente no plano de Argand-Gauss os números complexos:

Resolução
Cada complexo será um ponto no plano cuja abscissa é a parte real e a ordenada é a parte imaginária:

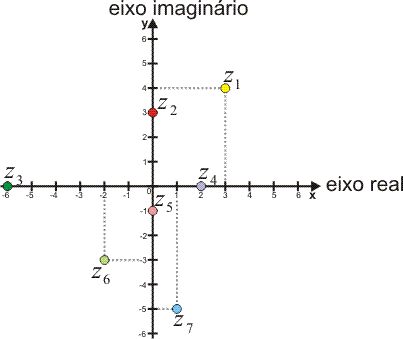
Note que os números reais estão localizados sobre o eixo real, assim como os números imaginários puros estão sobre o eixo imaginário.

Observação: Não é definida para o campo dos números complexos a relação de ordem, isto é, não existe um número complexo maior ou menor que outro.