Potenciação e radiciação de números complexos na forma trigonométrica

Potenciação

Sendo  e n um número inteiro maior que 1, temos:

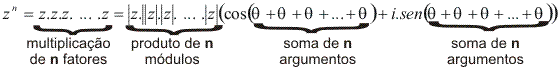
Assim:

Essa fórmula é conhecida como 1ª fórmula de Moivre.

Exemplo

Calcule :

Vamos considerar para posteriormente calcularmos . Para aplicar a 1ª fórmula de Moivre, precisamos calcular o módulo e o argumento de z.

Módulo:

Argumento: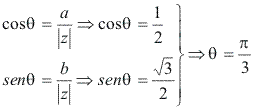

Calculando :

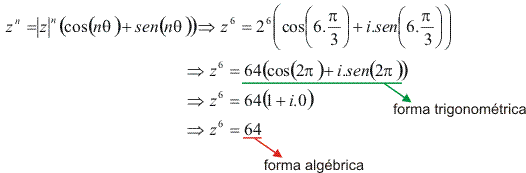
Radiciação

Se , suas raízes enésimas são dadas por:

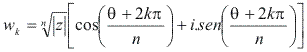Essa expressão é conhecida como 2ª fórmula de Moivre.

Exemplo

Determine as raízes cúbicas de z = 8.

Resolução

Vamos calcular o módulo e o argumento de z para a aplicação da 2ª fórmula de Moivre:

Módulo:

Argumento: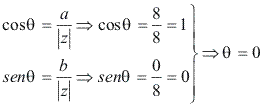

As raízes cúbicas de 8 são dadas por:

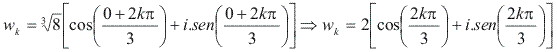
O número k pode assumir os valores 0, 1 e 2:

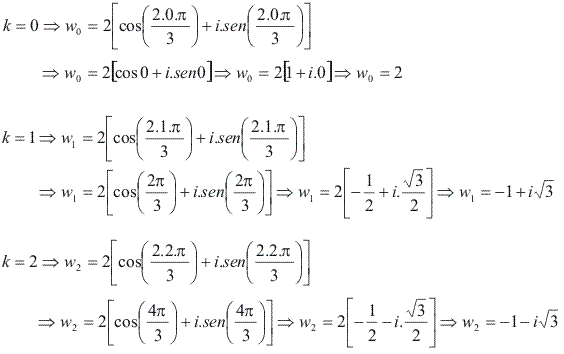
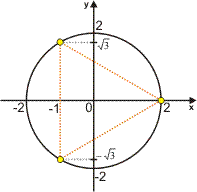
Geometricamente, note que as três raízes estão sobre uma circunferência de raio 2 e são vértices de um triângulo equilátero; seus argumentos formam uma PA, cujo primeiro termo é 0 e a razão é.