Você está em Ensino médio > Números complexos ▼
📄 Introdução e forma algébrica
📄 Igualdade de números complexos
📄 Conjugado de um número complexo
📄 Adição e subtração na forma algébrica
📄 Multiplicação e divisão na forma algébrica
📄 Potências de i
📄 Módulo e argumento
📄 Forma trigonométrica ou polar
📄 Multiplicação e divisão na forma trigonométrica
📄 Potenciação e radiciação na forma trigonométrica
📄 Igualdade de números complexos
📄 Conjugado de um número complexo
📄 Adição e subtração na forma algébrica
📄 Multiplicação e divisão na forma algébrica
📄 Potências de i
📄 Módulo e argumento
📄 Forma trigonométrica ou polar
📄 Multiplicação e divisão na forma trigonométrica
📄 Potenciação e radiciação na forma trigonométrica
Módulo e argumento de um número complexo
Considere o número complexo z = a + bi e o ponto P que o representa.
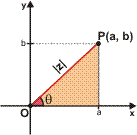
A distância de P até a origem é denominada módulo de z, e representada por ![]() . Do triângulo retângulo destacado temos:
. Do triângulo retângulo destacado temos:
A medida do ângulo ![]() , formado por
, formado por ![]() com o eixo das abscissas, medido no sentido anti-horário, é denominada argumento do complexo z. Note que
com o eixo das abscissas, medido no sentido anti-horário, é denominada argumento do complexo z. Note que ![]() .
.
Indica-se:
Note que:
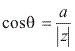 e
e 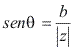
Exemplo
Determine o módulo e o argumento de ![]() .
.
Resolução:
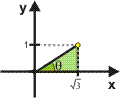
Módulo:
![]()
Argumento:
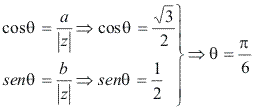
Próximo: Forma trigonométrica ou polar
Como referenciar: "Números complexos" em Só Matemática. Virtuous Tecnologia da Informação, 1998-2025. Consultado em 31/03/2025 às 07:43. Disponível na Internet em https://www.somatematica.com.br/emedio/complexos/complexos7.php





























