Conjugado de um número complexo

Sendo z = a + bi, define-se como conjugado de z o complexo = a – bi, ou seja:

z = a + bi = a – bi

Na prática, para se obter o conjugado de um número complexo, trocamos o sinal do coeficiente da parte imaginária.

Exemplos

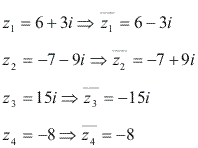
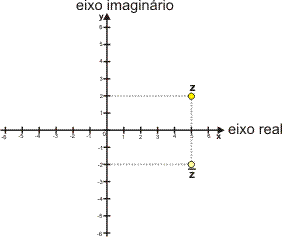
Geometricamente, podemos observar que dois números complexos conjugados têm, respectivamente, partes reais iguais e partes imaginárias simétricas.

Exemplo

z = 5 + 2i e seu conjugado = 5 -2i