|
Retas
Geometria analítica: retas
Introdução
Entre
os pontos de uma reta e os números reais existe uma correspondência
biunívoca, isto é, a cada ponto de reta corresponde um único número real e
vice-versa.
Considerando uma reta
horizontal x, orientada da esquerda para direita (eixo), e determinando
um ponto O dessa reta ( origem) e um segmento u, unitário e
não-nulo, temos que dois números inteiros e consecutivos determinam sempre
nesse eixo um segmento de reta de comprimento u:
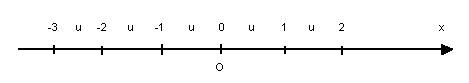
Medida algébrica de um
segmento
Fazendo
corresponder a dois pontos, A e B, do eixo x os números reais xA
e xB , temos:
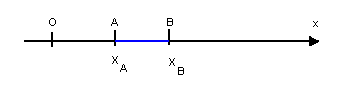
A medida algébrica de um segmento
orientado é o número real que corresponde à diferença entre as abscissas da
extremidade e da origem desse segmento.
Plano cartesiano
A
geometria analítica teve como principal idealizador o filósofo francês René
Descartes ( 1596-1650). Com o auxílio de um sistema de eixos associados a um
plano, ele faz corresponder a cada ponto do plano um par ordenado e vice-versa.
Quando os eixos desse
sistemas são perpendiculares na origem, essa correspondência determina um
sistema cartesiano ortogonal ( ou plano cartesiano). Assim, há uma
reciprocidade entre o estudo da geometria ( ponto, reta, circunferência) e da
Álgebra ( relações, equações etc.), podendo-se representar graficamente
relações algébricas e expressar algebricamente representações gráficas.
Observe o plano cartesiano
nos quadros quadrantes:
Exemplos:
- A(2, 4) pertence ao 1º quadrante (xA
> 0 e yA > 0)
- B(-3, -5) pertence ao 3º quadrante ( xB
< 0 e yB < 0)
Observação: Por convenção, os pontos localizados sobre
os eixos não estão em nenhum quadrante.
Distância entre dois pontos
Dados
os pontos A(xA, yA) e B(xB, yB)
e sendo dAB a distância entre eles, temos:
Aplicando o teorema de
Pitágoras ao triângulo retângulo ABC, vem:
Como exemplo, vamos determinar a distância
entre os pontos A(1, -1) e B(4, -5):
<<
Voltar para Ensino médio
|
