Representação gráfica de retas

Para representar graficamente as retas de equação ax + by + c = 0 ( b0), isolamos a variável y e atribuímos valores a x, obtendo pares ordenados que são pontos da reta. Assim, é mais conveniente usar a equação na forma reduzida, já que ela apresenta o y isolado.

Coordenadas do ponto de intersecção de retas

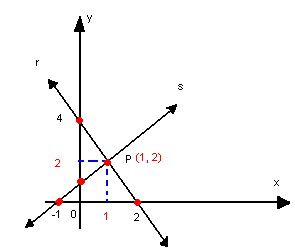
A intersecção das retas r e s, quando existir, é o ponto P(x, y), comum a elas, que é a solução do sistema formado pelas equações das duas retas. Vamos determinar o ponto de intersecção, por exemplo, das retas r: 2x +y - 4 =0 e s: x -y +1=0. Montando o sistema e resolvendo-o, temos:

Substituindo esse valor em x -y = -1, temos:

1 - y = -1

y = 2

Logo, P(1, 2) é o ponto de intersecção das retas r e s.

Graficamente, temos: