Condições de alinhamento de três pontos

Se três pontos, A(x_A, y_A), B(x_B, y_B) e C(x_C, y_C), estão alinhados, então:

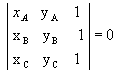
Para demonstrar esse teorema podemos considerar três casos:

a) três pontos alinhados horizontalmente

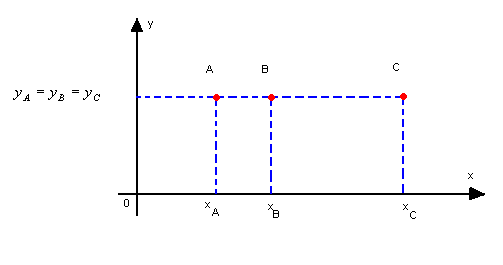
Neste caso, as ordenadas são iguais:

y_A = y_B = y_C

e o determinante é nulo, pois a 2ª e a 3ª coluna são proporcionais.

b) três pontos alinhados verticalmente

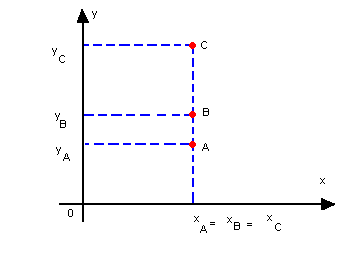
Neste caso, as abscissas são iguais:

x_A = x_B = x_C

 e o determinante é nulo, pois a 1ª e a 3ª coluna são proporcionais.

c) três pontos numa reta não-paralela aos eixos

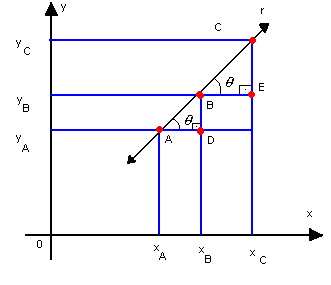
Pela figura, verificamos que os triângulos ABD e BCE são semelhantes. Então:

Desenvolvendo, vem:

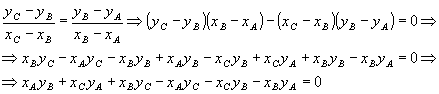
Como:

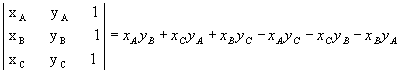
então .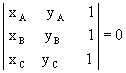

Observação: A recíproca da afirmação demonstrada é válida, ou seja, se 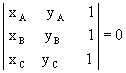, então os pontos A(x_A,y_A), B(x_B,y_B) e C(x_C, y_C) estão alinhados.